Kącik Wiedzy
Belka statycznie wyznaczalna - przykład krok po kroku

Belka statycznie wyznaczalna - przykład krok po kroku

maja 21, 2018

Wprowadzenie

Zadanie: Obliczyć reakcje podporowe i siły wewnętrzne w belce statycznie wyznaczalnej.

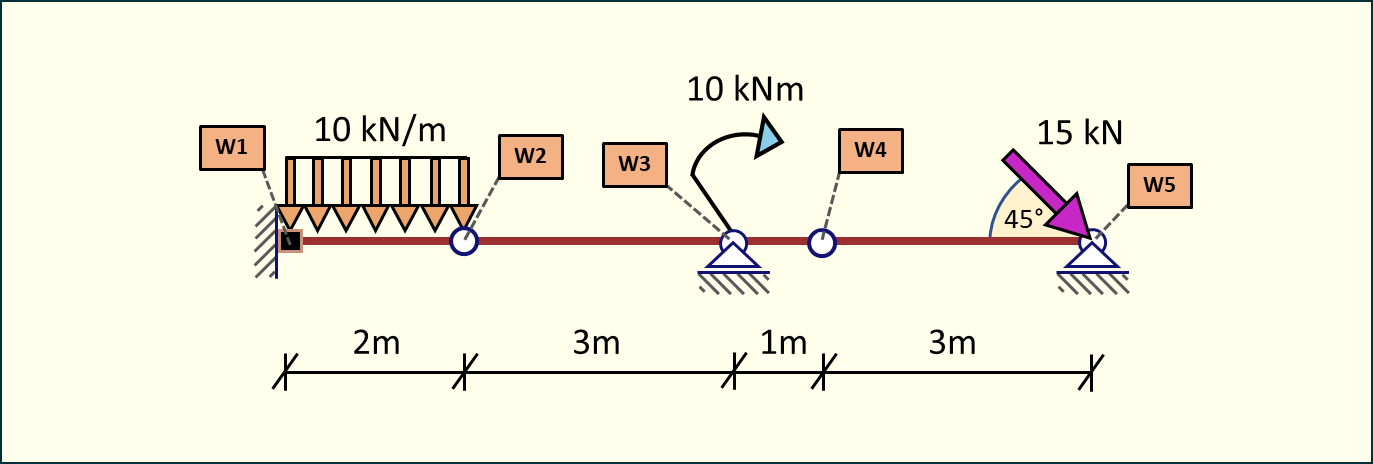
Rys. 1. Schemat statyczny belki

1. Stopień statycznej niewyznaczalności

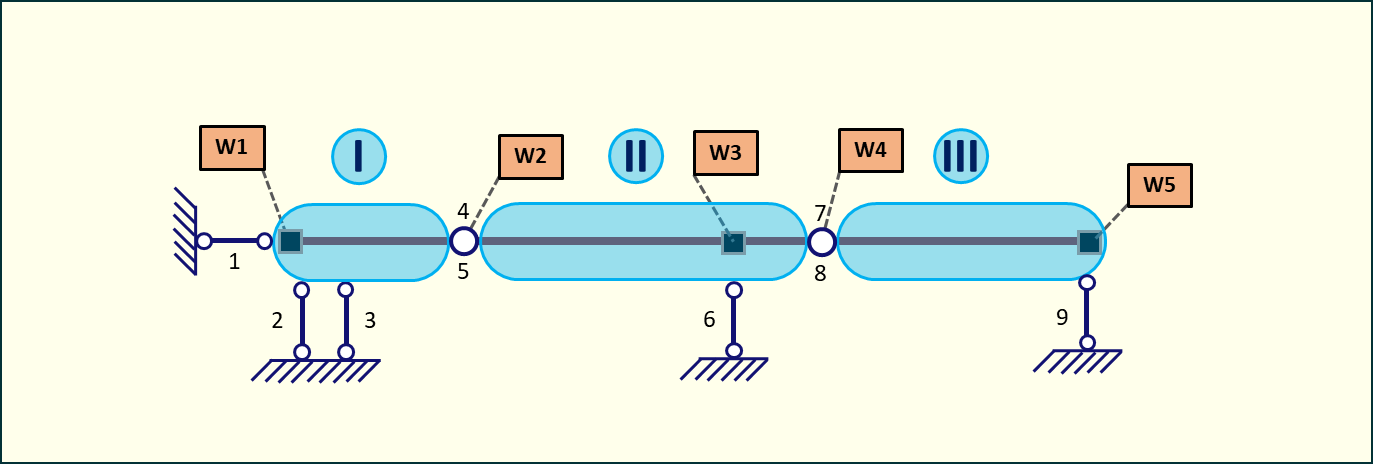
Rys. 2. Analiza stopnia statycznej niewyznaczalności

Liczba tarcz = 3
Liczba więzi = 9
3t = w
3 x 3 = 9
9 = 9

Warunek spełniony. Układ jest statycznie wyznaczalny.

2. Reakcje podporowe

Suma momentów w przegubie jest równa zero. Korzystając z tego faktu możemy wyznaczyć reakcje podporowe rozkładając belkę na tarcze i układając odpowiednie równania.

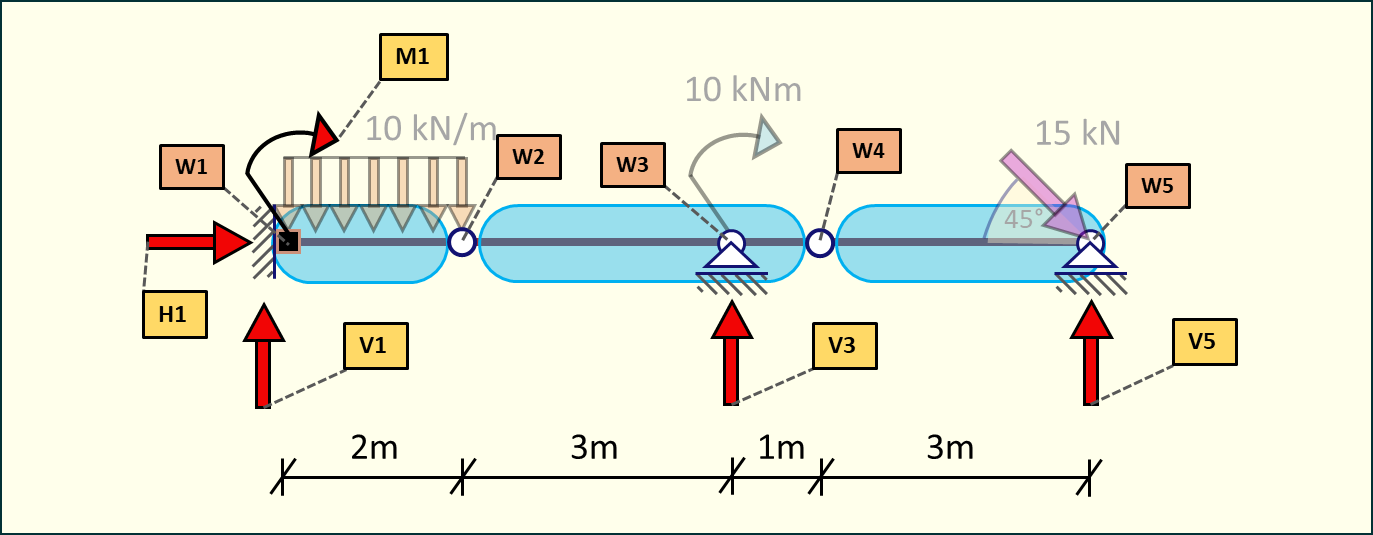
Rys. 3. Rozkład belki na tarcze

Najpierw policzymy reakcję pionową w węźle nr 5, obliczając sumę momentów względem węzła nr 4 dla tarczy nr III.

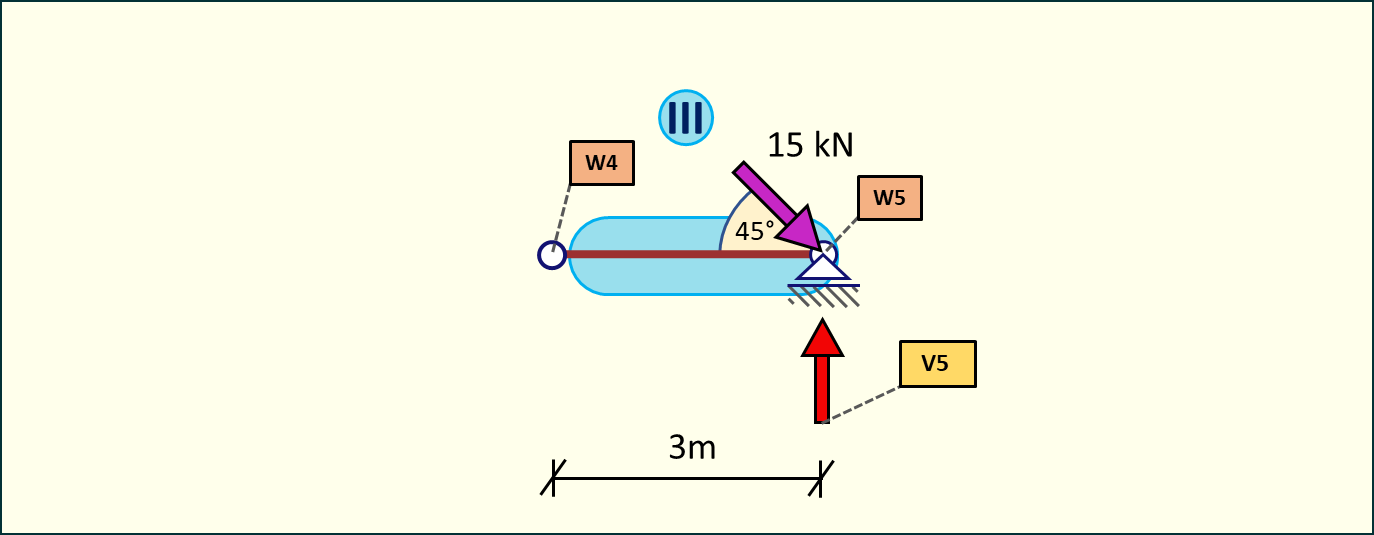
Rys. 4. Obliczenie reakcji V5 - tarcza nr III

M4=0M_4 = 0

−V5⋅3 m+15⋅sin⁡(45°)⋅3 m=0-V_5 \cdot 3\,\text{m} + 15 \cdot \sin(45°) \cdot 3\,\text{m} = 0

V5=10,61 kNV_5 = 10{,}61\,\text{kN}

Następnie dodajemy drugą tarczę i liczymy reakcję w węźle nr 3 obliczając sumę momentów względem węzła nr 2.

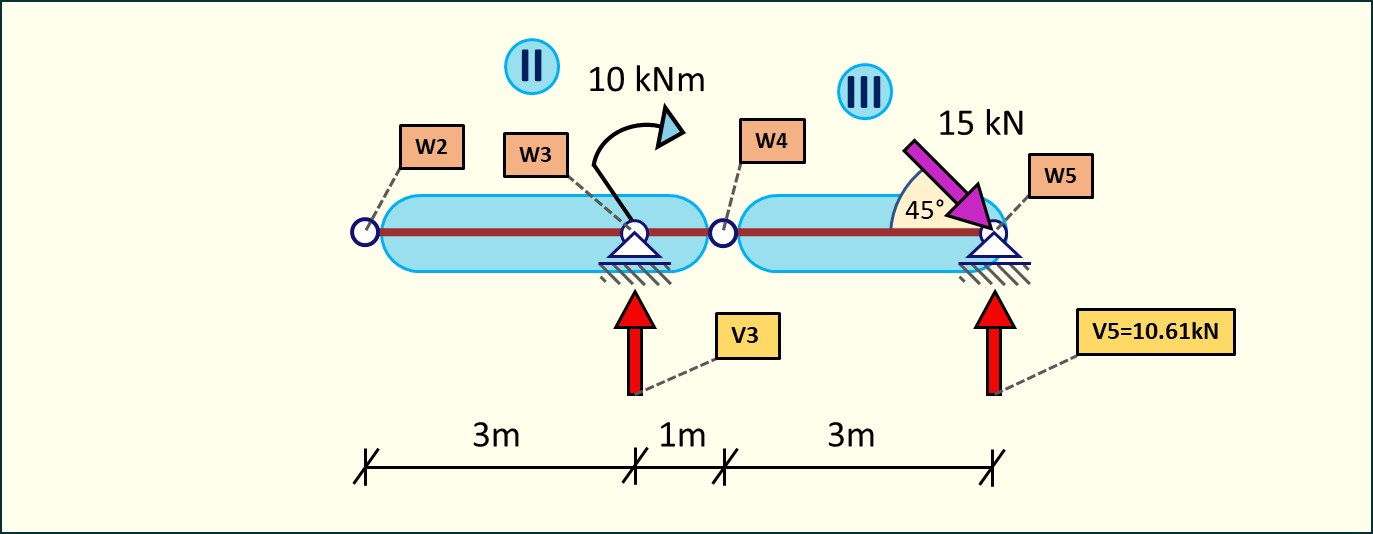
Rys. 5. Obliczenie reakcji V3 - tarcze II i III

∑M2=0\sum M_2 = 0

−V3⋅3 m+10 kNm+15 kN⋅sin⁡(45°)⋅7 m−V5⋅7 m=0-V_3 \cdot 3\,\text{m} + 10\,\text{kNm} + 15\,\text{kN} \cdot \sin(45°) \cdot 7\,\text{m} - V_5 \cdot 7\,\text{m} = 0

−3V3+10 kNm+10,61 kN⋅7 m−10,61 kN⋅7 m=0-3V_3 + 10\,\text{kNm} + 10{,}61\,\text{kN} \cdot 7\,\text{m} - 10{,}61\,\text{kN} \cdot 7\,\text{m} = 0

3V3=10 kN3V_3 = 10\,\text{kN}

V3=3,33 kNV_3 = 3{,}33\,\text{kN}

Ostatnim krokiem jest rozpatrzenie całej belki i wyznaczenie reakcji we wsporniku korzystając z warunków równowagi.

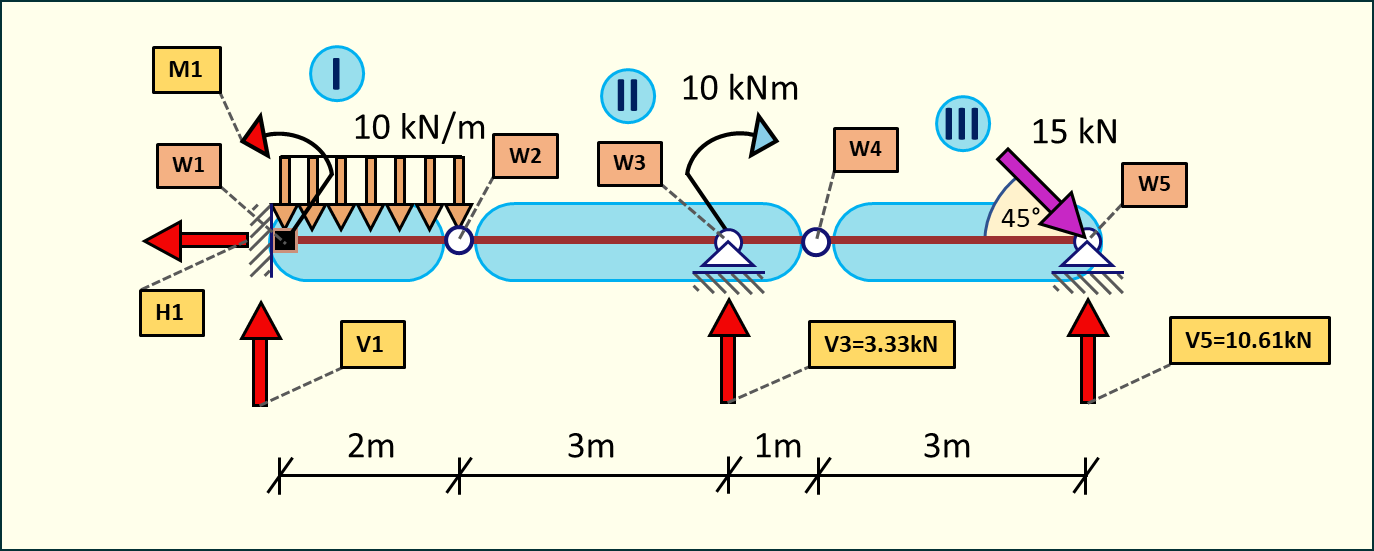
Rys. 6. Obliczenie reakcji we wsporniku - cała belka

∑Py=0\sum P_y = 0

−H1+15 kN⋅cos⁡(45°)=0-H_1 + 15\,\text{kN} \cdot \cos(45°) = 0

H1=10,61 kNH_1 = 10{,}61\,\text{kN}
∑Px=0\sum P_x = 0

V1−10 kN/m⋅2 m+V3+V5−15 kN⋅sin⁡(45°)=0V_1 - 10\,\text{kN/m} \cdot 2\,\text{m} + V_3 + V_5 - 15\,\text{kN} \cdot \sin(45°) = 0

V1−20 kN+3,33 kN+10,61 kN−10,61 kN=0V_1 - 20\,\text{kN} + 3{,}33\,\text{kN} + 10{,}61\,\text{kN} - 10{,}61\,\text{kN} = 0

V1=16,67 kNV_1 = 16{,}67\,\text{kN}
∑M4=0\sum M_4 = 0

−M1+V1⋅6 m−10 kN/m⋅2 m⋅5 m+V3⋅1 m+15 kN⋅sin⁡(45°)⋅3 m−V5⋅3 m=0-M_1 + V_1 \cdot 6\,\text{m} - 10\,\text{kN/m} \cdot 2\,\text{m} \cdot 5\,\text{m} + V_3 \cdot 1\,\text{m} + 15\,\text{kN} \cdot \sin(45°) \cdot 3\,\text{m} - V_5 \cdot 3\,\text{m} = 0

−M1+6 m⋅16,67 kN−100 kNm+10 kNm+3,33 kNm+31,82 kNm−31,82 kNm=0-M_1 + 6\,\text{m} \cdot 16{,}67\,\text{kN} - 100\,\text{kNm} + 10\,\text{kNm} + 3{,}33\,\text{kNm} + 31{,}82\,\text{kNm} - 31{,}82\,\text{kNm} = 0

M1=100 kNm−100 kNm+10 kNm+3,33 kNmM_1 = 100\,\text{kNm} - 100\,\text{kNm} + 10\,\text{kNm} + 3{,}33\,\text{kNm}

M1=13,33 kNmM_1 = 13{,}33\,\text{kNm}

3. Siły wewnętrzne

Następnym krokiem jest obliczenie sił wewnętrznych w belce. W tym celu musimy ciąć belkę w miejscach przyłożenia sił i układać równania do wyliczenia sił wewnętrznych.

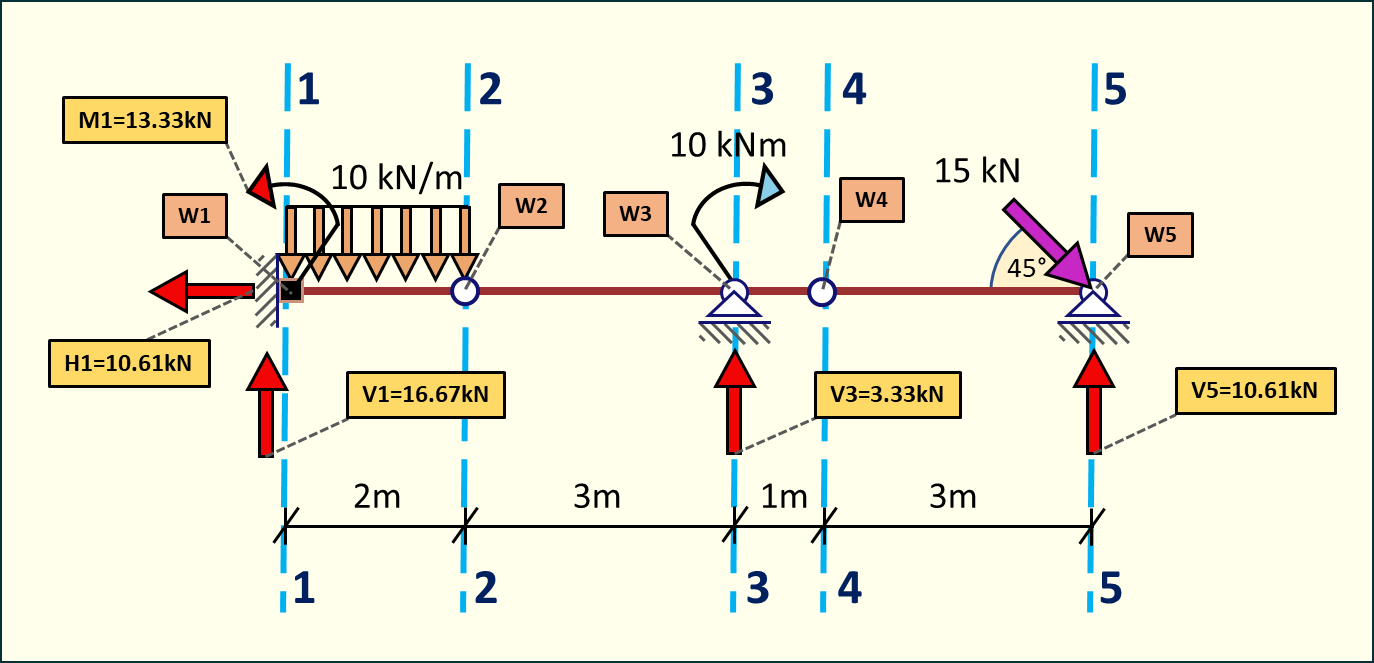
Rys. 7. Schemat cięć belki do wyznaczania sił wewnętrznych

3.1. Momenty

Do obliczania momentów potrzebne nam są tylko siły pionowe i momenty skupione. Pomijamy wszelkie siły poziome, ponieważ przechodzą one przez oś belki. Oznacza to, że ramię działania tych sił wynosi zero, a co za tym idzie, moment działający na belkę od pochodzący od tych rownież wynosi zero.

Przedział 1-2 0<x<2

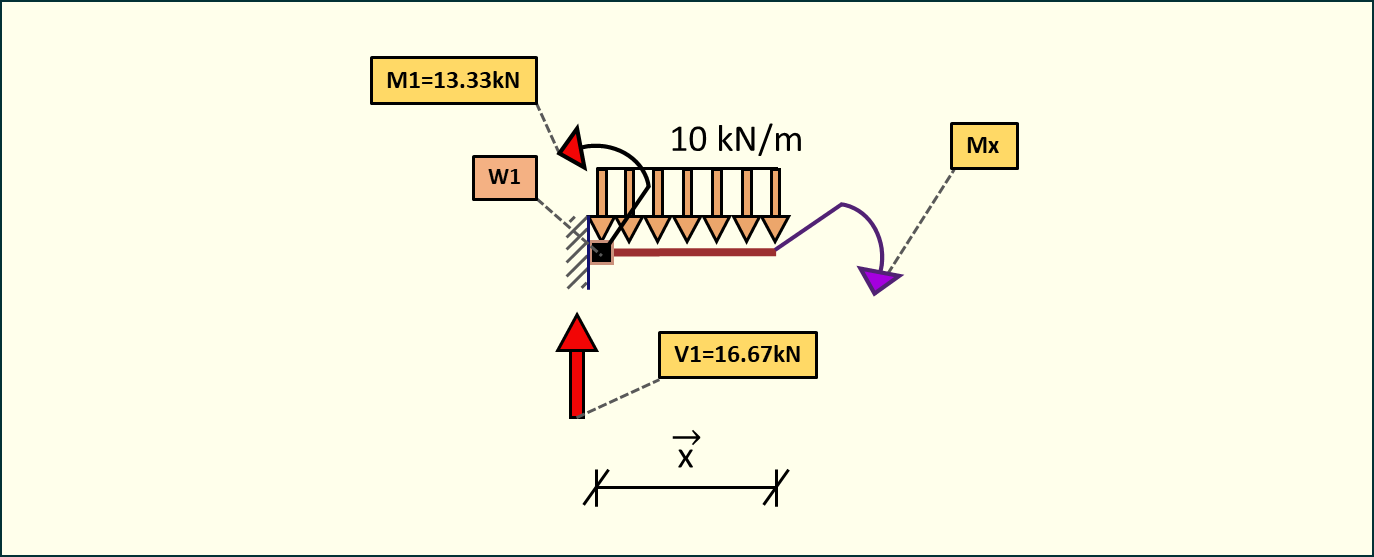
Rys. 8. Przekrój belki - momenty w przedziale 1-2

MX+16,67 kN⋅x−13,33 kN−10 kN/m⋅x⋅12x=0M_X + 16{,}67\,\text{kN} \cdot x - 13{,}33\,\text{kN} - 10\,\text{kN/m} \cdot x \cdot \frac{1}{2}x = 0

MX=5x2−16,67x+13,33M_X = 5x^2 - 16{,}67x + 13{,}33

Otrzymaliśmy funkcję kwadratową, więc konieczne jest policzenie miejsc zerowych tej funkcji aby móc narysować jej wykres. Musimy pamiętać, że wykres funkcji kwadratowej nie jest linią prostą, lecz parabolą. Do policzenia miejsc zerowych potrzebne nam będą podstawowe wzory matematyczne.

5x2−16,67x+13,33=05x^2 - 16{,}67x + 13{,}33 = 0

Δ=b2−4ac=(−16,67)2−4⋅5⋅13,33=11,29\Delta = b^2 - 4ac = (-16{,}67)^2 - 4 \cdot 5 \cdot 13{,}33 = 11{,}29

Δ=3,36\sqrt{\Delta} = 3{,}36

x1=−b+Δ2a=16,67+3,362⋅5=2x_1 = \frac{-b + \sqrt{\Delta}}{2a} = \frac{16{,}67 + 3{,}36}{2 \cdot 5} = 2

x2=−b−Δ2a=16,67−3,362⋅5=1,33x_2 = \frac{-b - \sqrt{\Delta}}{2a} = \frac{16{,}67 - 3{,}36}{2 \cdot 5} = 1{,}33

Mamy zatem dwa miejsca zerowe. Jedno w odległości 1.33 metra od wspornika, a drugie na przegubie. Dla x = 0 wartość funkcji wynosi:

5⋅02−16,67⋅0+13,33=13,33 kNm5 \cdot 0^2 - 16{,}67 \cdot 0 + 13{,}33 = 13{,}33\,\text{kNm}

Jest to wartość momentu we wsporniku.

Przedział 4-5 0<x<3

Policzymy to od końca belki, ponieważ uprości to obliczenia. Mamy do rozpatrzenia fragment belki, na którym występują tylko dwie siły.

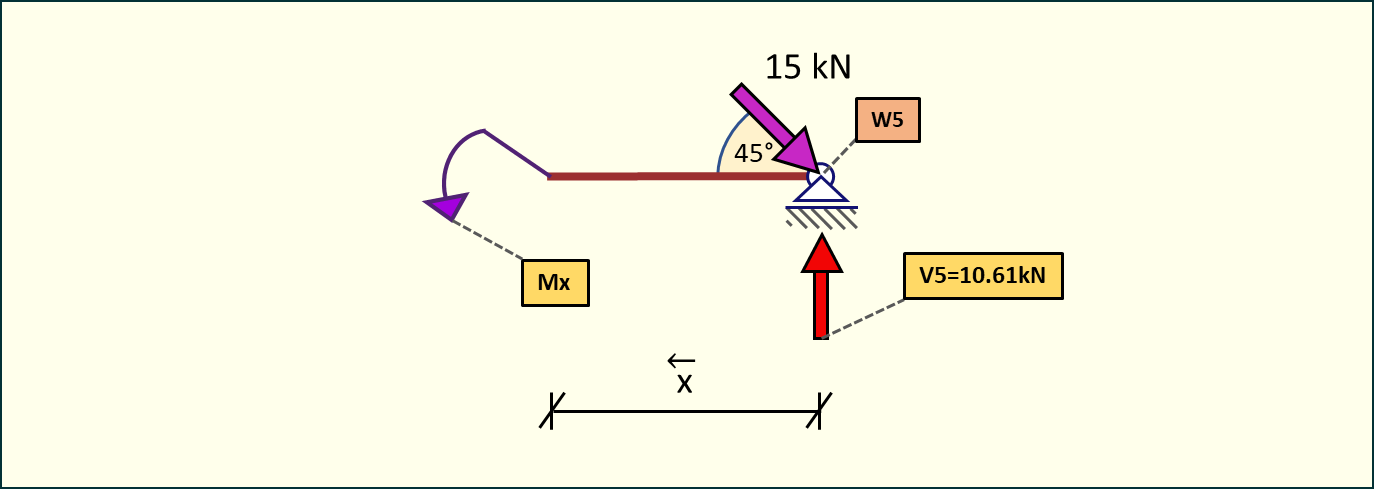
Rys. 9. Przekrój belki - momenty w przedziale 4-5

−MX+x⋅15 kN⋅sin⁡(45°)−V5⋅x=0-M_X + x \cdot 15\,\text{kN} \cdot \sin(45°) - V_5 \cdot x = 0

MX=0M_X = 0

Na tym odcinku nie występują żadne momenty zginające.

Przedział 1-2

Do obliczenia środkowej części belki musimy znać siły w pierwszym przegubie od strony wspornika.

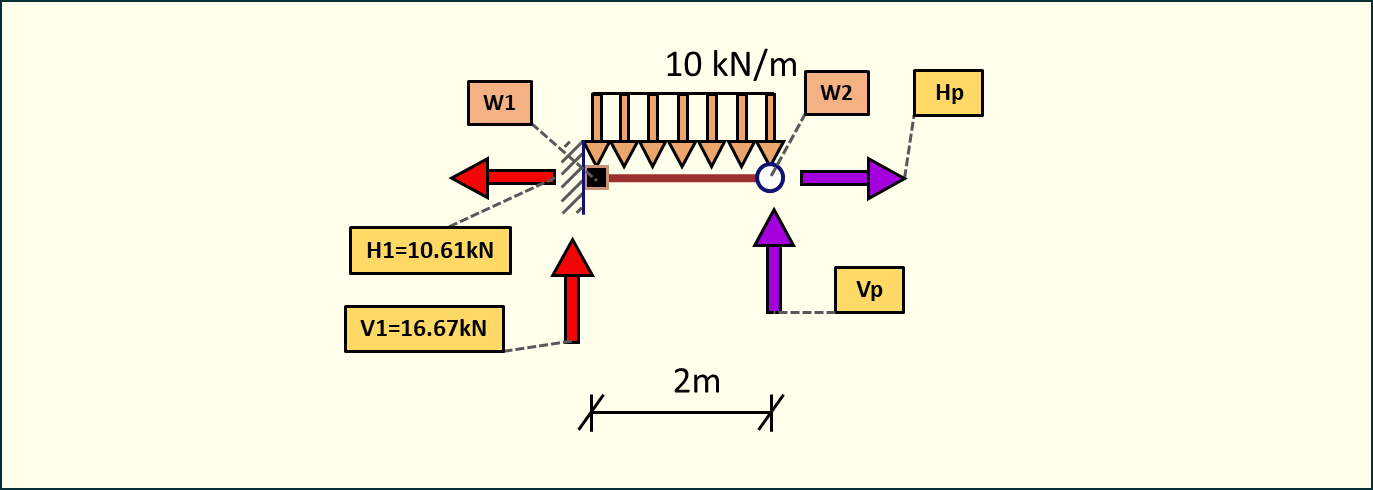
Rys. 10. Przekrój belki - siły w przegubie w przedziale 1-2

∑Px=0\sum P_x = 0

V1−2m⋅10 kN/m+VP=0V_1 - 2\text{m} \cdot 10\,\text{kN/m} + V_P = 0

16,67 kN−2 m⋅10 kN/m+VP=016{,}67\,\text{kN} - 2\,\text{m} \cdot 10\,\text{kN/m} + V_P = 0

VP=3,33 kNV_P = 3{,}33\,\text{kN}
∑Y=0\sum Y = 0

−H1+HP=0-H_1 + H_P = 0

Hp=10,61 kNH_p = 10{,}61\,\text{kN}

Przedział 2-4 0<x<3

Znając reakcje w przegubie możemy obliczyć momenty w środkowej części belki.

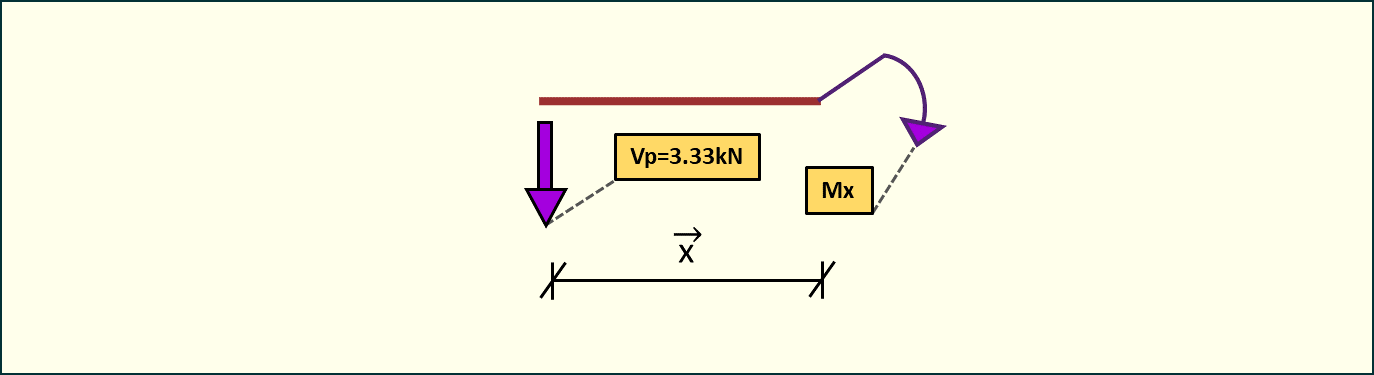
Rys. 11. Przekrój belki - momenty w przedziale 2-4

MX−VP⋅x=0M_X - V_P \cdot x = 0

MX=−x⋅VPM_X = -x \cdot V_P

MX=−3,33xM_X = -3{,}33x

Obliczmy wartość momentu na podporze:

M3=−3,33⋅3=−10 kNM_3 = -3{,}33 \cdot 3 = -10\,\text{kN}

Na podporze występuje moment skupiony, który redukuje wykres momentów do zera, ponieważ jest przeciwnego znaku.

Zatem nasz wykres momentów będzie wyglądał następująco:

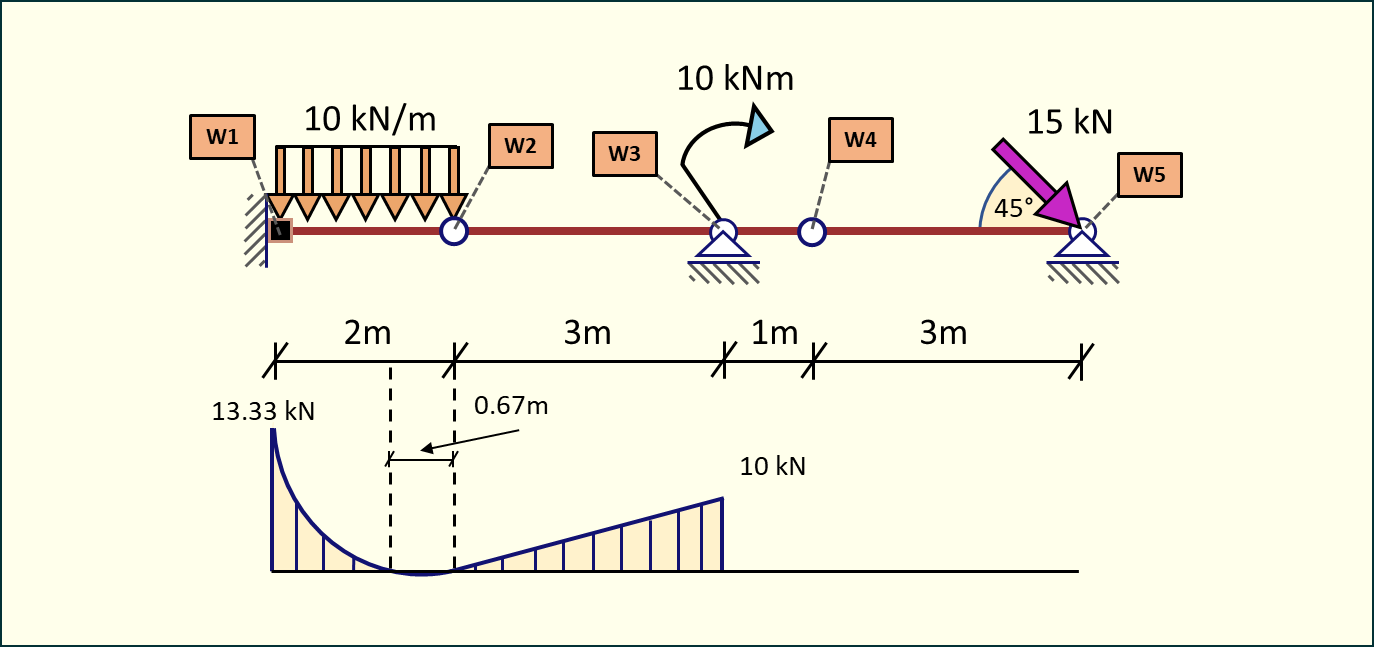
Rys. 12. Wykres momentów zginających

3.2. Siły tnące

Do obliczania sił tnących potrzebne nam są tylko siły pionowe.

Przedział 1-2 0<x<2

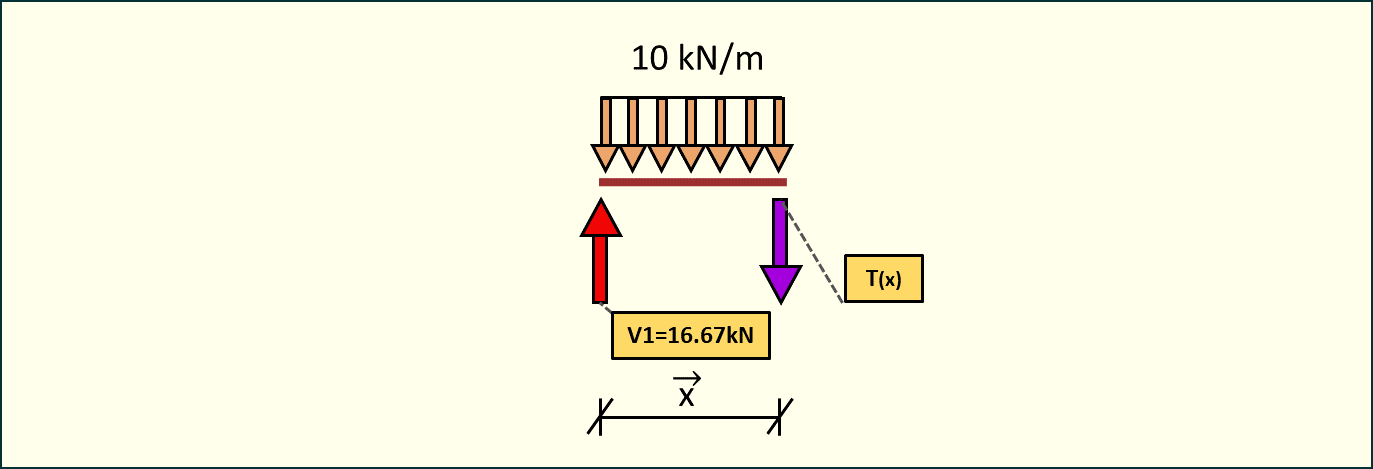
Rys. 13. Przekrój belki - siły tnące w przedziale 1-2

−V1+10 kN/m⋅x+T(x)=0-V_1 + 10\,\text{kN/m} \cdot x + T_{(x)} = 0

T(x)=+V1−10xT_{(x)} = +V_1 - 10x

T(x)=−10x+16,67T_{(x)} = -10x + 16{,}67

T(0)=−10⋅0+16,67T_{(0)} = -10 \cdot 0 + 16{,}67

T(0)=16,67 kNT_{(0)} = 16{,}67\,\text{kN}

T(2)=−10⋅2+16,67=−3,33 kNT_{(2)} = -10 \cdot 2 + 16{,}67 = -3{,}33\,\text{kN}

Przedział 2-4 0<x<4

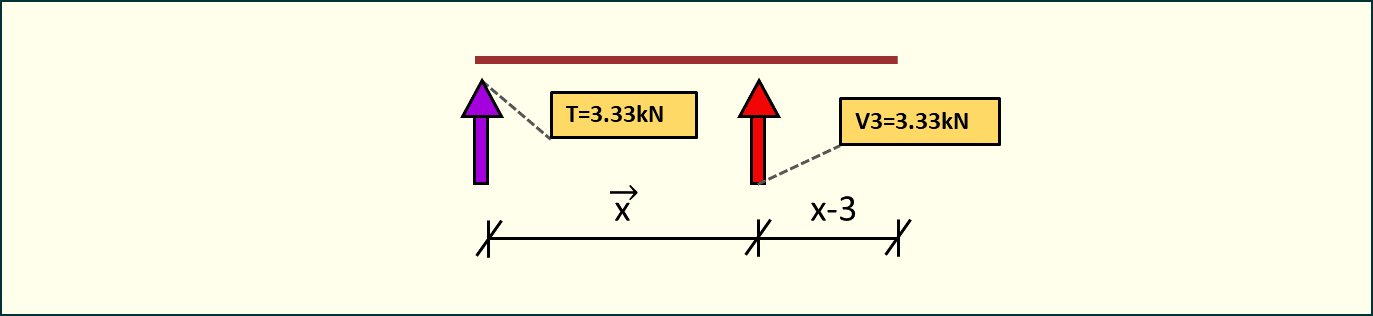
Rys. 14. Przekrój belki - siły tnące w przedziale 2-4

−T(x)−V3=0-T_{(x)} - V_3 = 0

T(x)=−VPT_{(x)} = -V_P

T(x)=−3,33 kNT_{(x)} = -3{,}33\,\text{kN}

Z rysunku widzimy, że wykres sił tnących będzie niezmienny do podpory, a na podporze następuje redukcja sił tnących do zera. Czyli od podpory wykres będzie zerowy.

Przedział 4-5 0<x<3

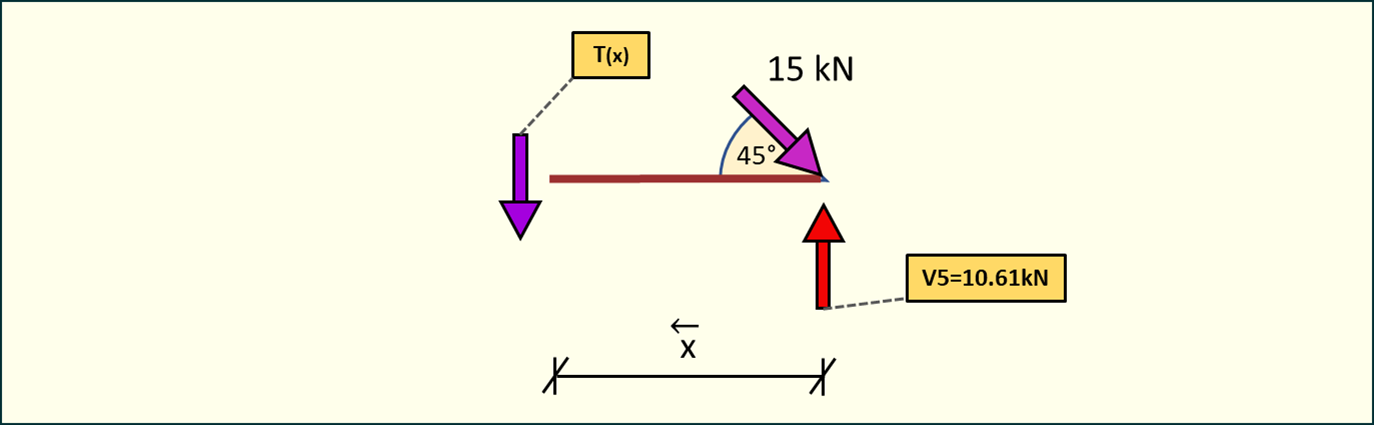
Rys. 15. Przekrój belki - siły tnące w przedziale 4-5

TX+15 kN⋅sin⁡(45°)−V5=0T_X + 15\,\text{kN} \cdot \sin(45°) - V_5 = 0

−V5+15 kN⋅sin⁡(45°)=−TX-V_5 + 15\,\text{kN} \cdot \sin(45°) = -T_X

TX=0T_X = 0

W tym przekroju belki nie wystepują żadne siły tnące.

Wykres sił tnących będzie prezentował się następująco:

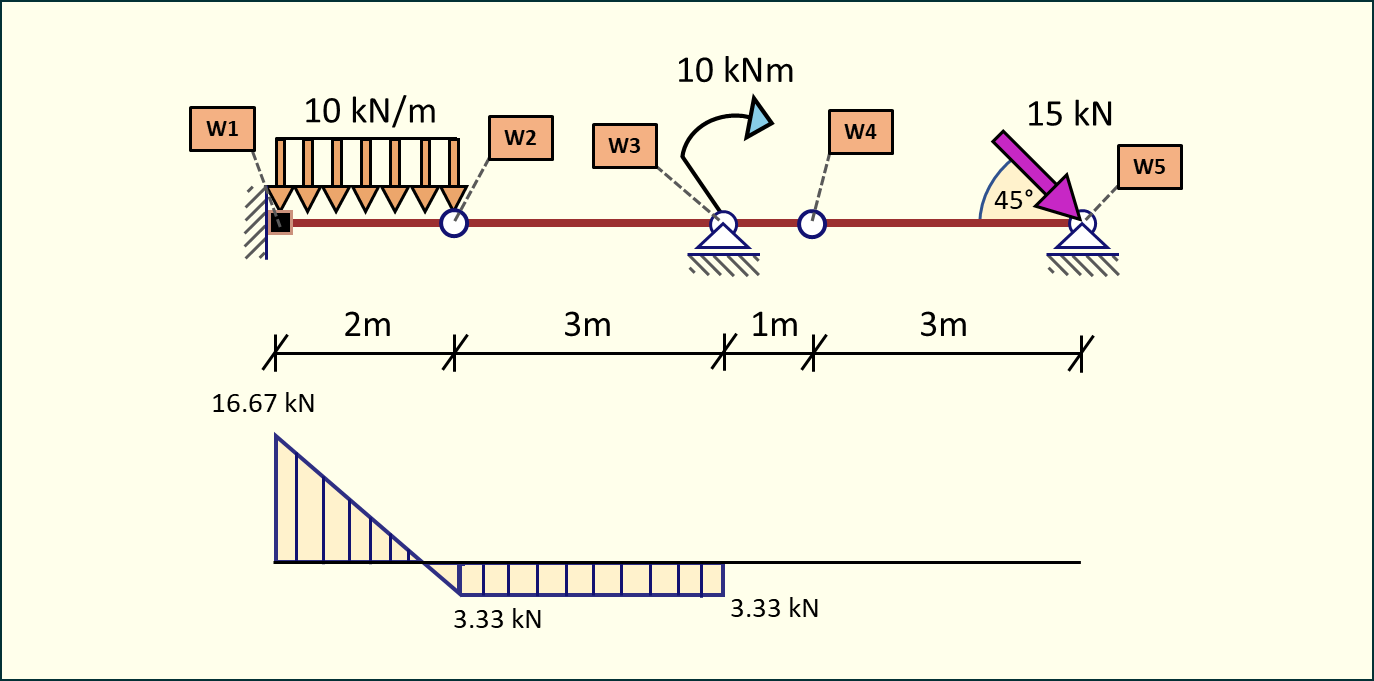
Rys. 16. Wykres sił tnących

3.3. Siły normalne

Do obliczenia sił normalnych będą nam potrzebne tylko siły poziome.

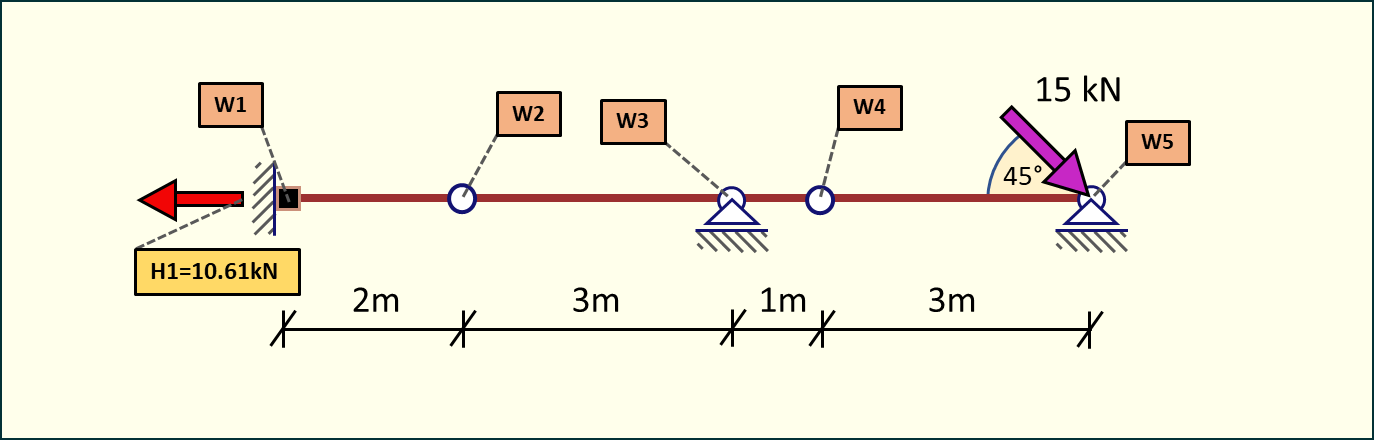
Rys. 17. Siły poziome działające na belkę

Z rysunku możemy odczytać, że w układzie występują tylko dwie siły poziome na obu końcach belki. Z tego wynika, że cały element będzie rozciągany, ponieważ siły będą przenoszone na każdą tarcze poprzez przeguby.

Nasz końcowy wykres sił normalnych będzie wyglądał następująco:

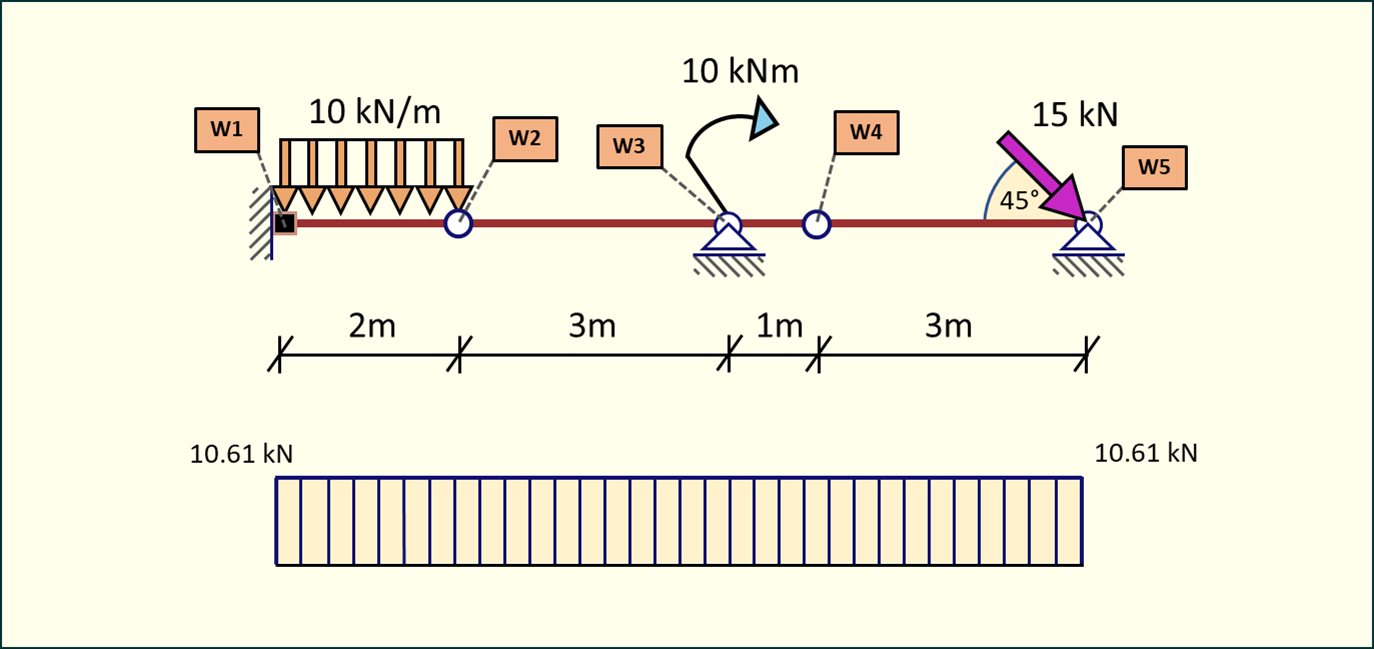
Rys. 18. Wykres sił normalnych

Ostatnia aktualizacja:
Wykresy sił wewnętrznych i ich wzory dla układów prostychRama statycznie wyznaczalna - krok po kroku