Funkcja kwadratowa
Funkcja kwadratowa jest jedną z najczęściej spotykanych funkcji matematycznych. Z tego powodu warto przyjrzeć się jej bliżej i zapoznać się z jej formą oraz własnościami.
Funkcję kwadratową opisać można równaniem:
Gdzie:
- – wartość funkcji
- – stałe funkcji
- – zmienna funkcji
Wykresem tej funkcji jest parabola, której ramiona mogą być skierowane w górę lub w dół w zależności od znaku stałej .
Kształt paraboli
Ramiona w górę ()
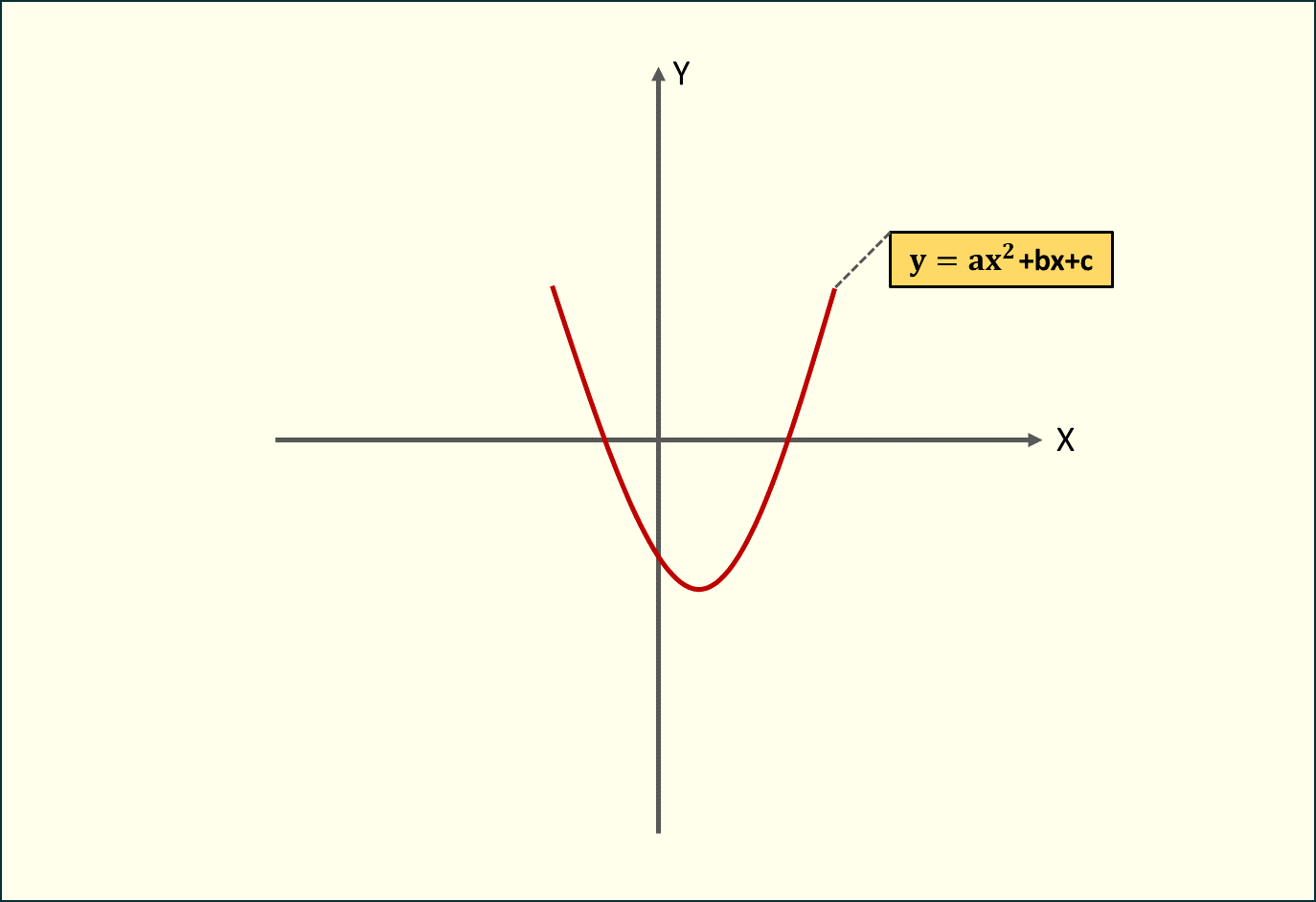
Rys. 1. Parabola z ramionami skierowanymi w górę (a > 0)
Ramiona w dół ()
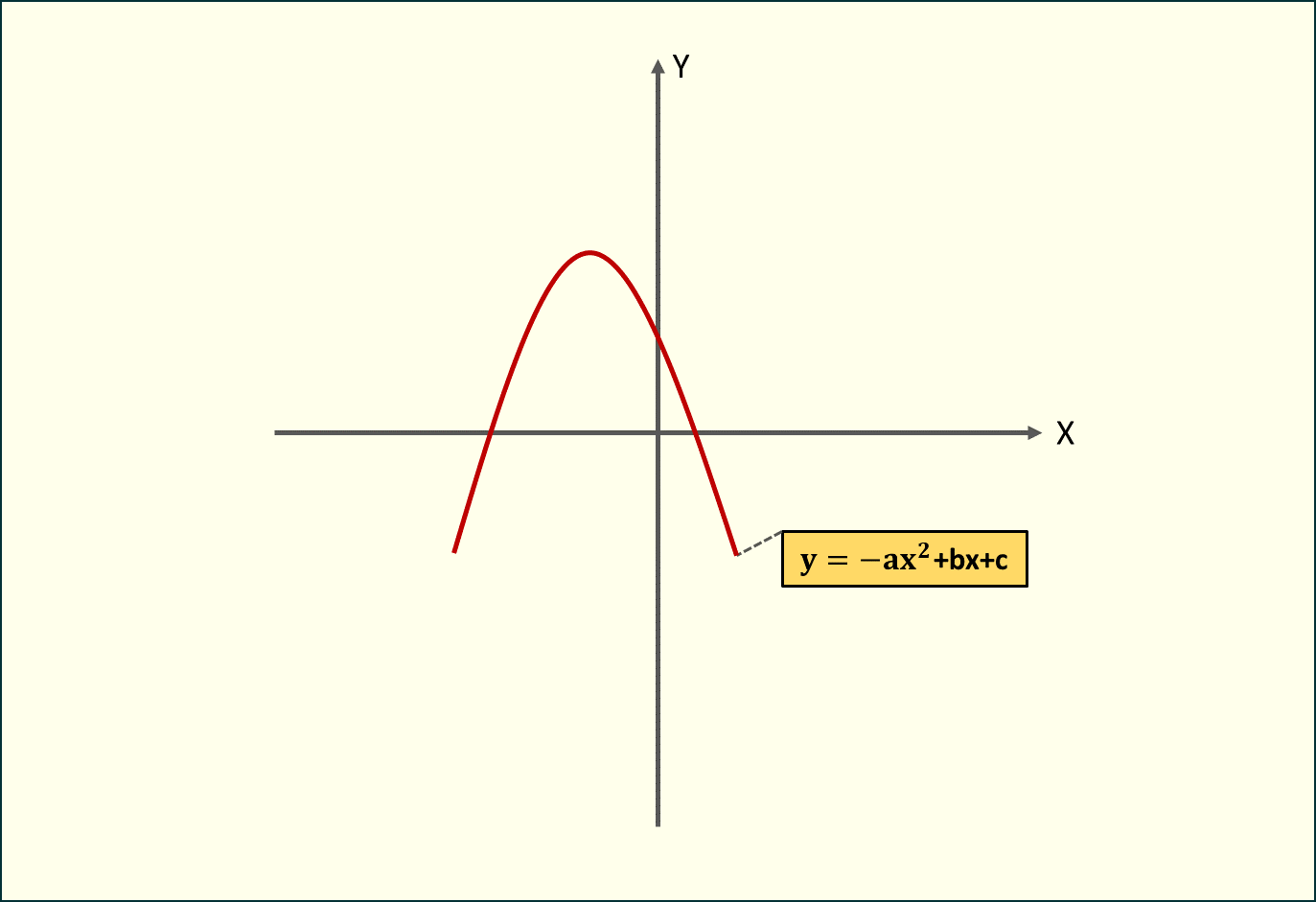
Rys. 2. Parabola z ramionami skierowanymi w dół (a < 0)
Jeżeli , to funkcja kwadratowa staje się liniową.
Miejsca zerowe funkcji
Aby określić miejsca zerowe funkcji kwadratowej, najpierw obliczamy wyróżnik (deltę):
gdzie:
- – wyróżnik funkcji kwadratowej
- – stałe funkcji kwadratowej
Kiedy obliczymy wyróżnik, możemy określić liczbę miejsc zerowych, czyli punktów przecięcia funkcji z osią :
- – brak miejsc zerowych
- – jedno miejsce zerowe
- – dwa miejsca zerowe
Aby kontynuować obliczenia, musimy znać pierwiastek z wyróżnika:
Następnie, korzystając ze wzorów, możemy obliczyć wartość zmiennej , dla której :
Ekstremum funkcji
Funkcja przyjmuje wartość ekstremalną dla argumentu:
Rodzaj ekstremum zależy od znaku stałej :
- – ekstremum będzie wartością maksymalną
- – ekstremum będzie wartością minimalną
Wartość ekstremalną liczymy ze wzoru:
Poniżej zobrazowano położenie ekstremum na wykresie:
Maksimum ()
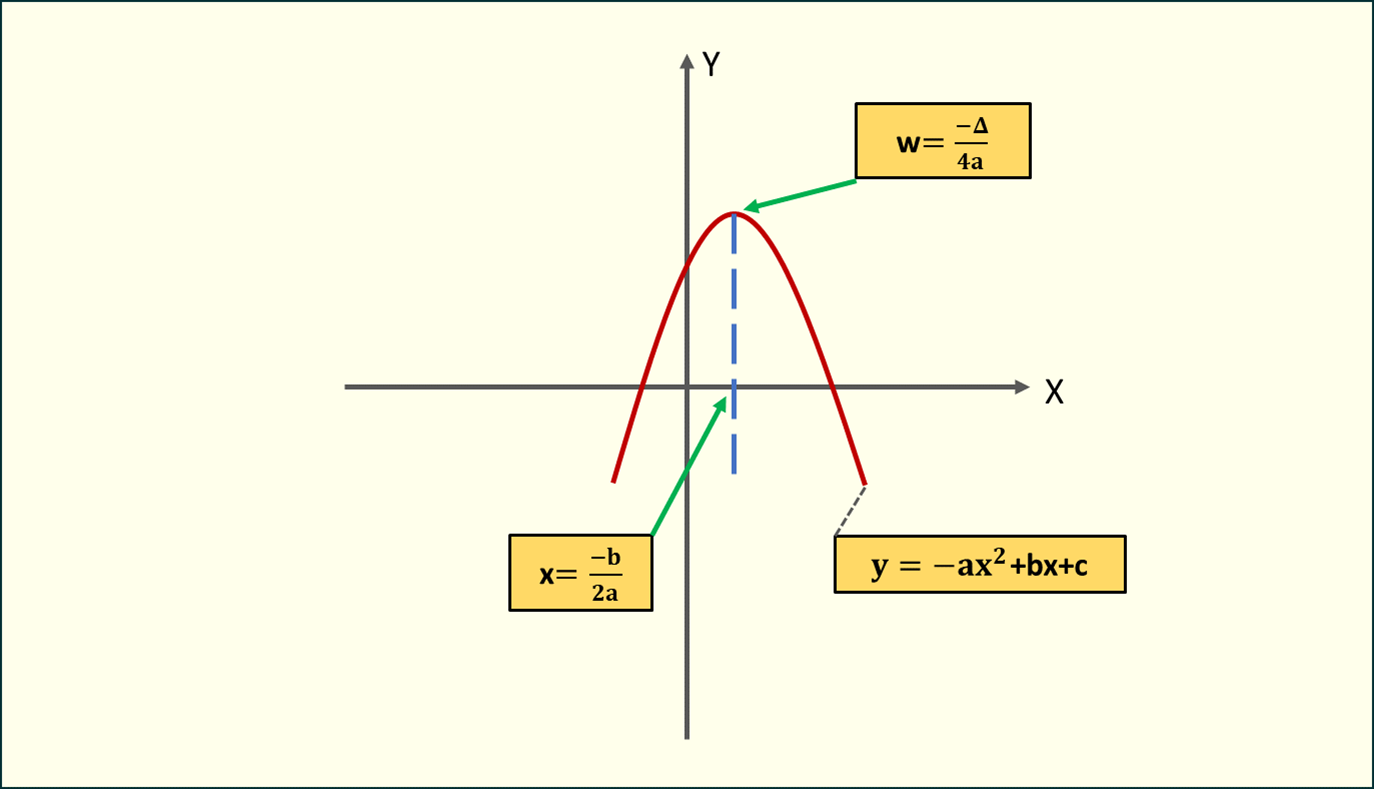
Rys. 3. Położenie maksimum funkcji kwadratowej
Minimum ()
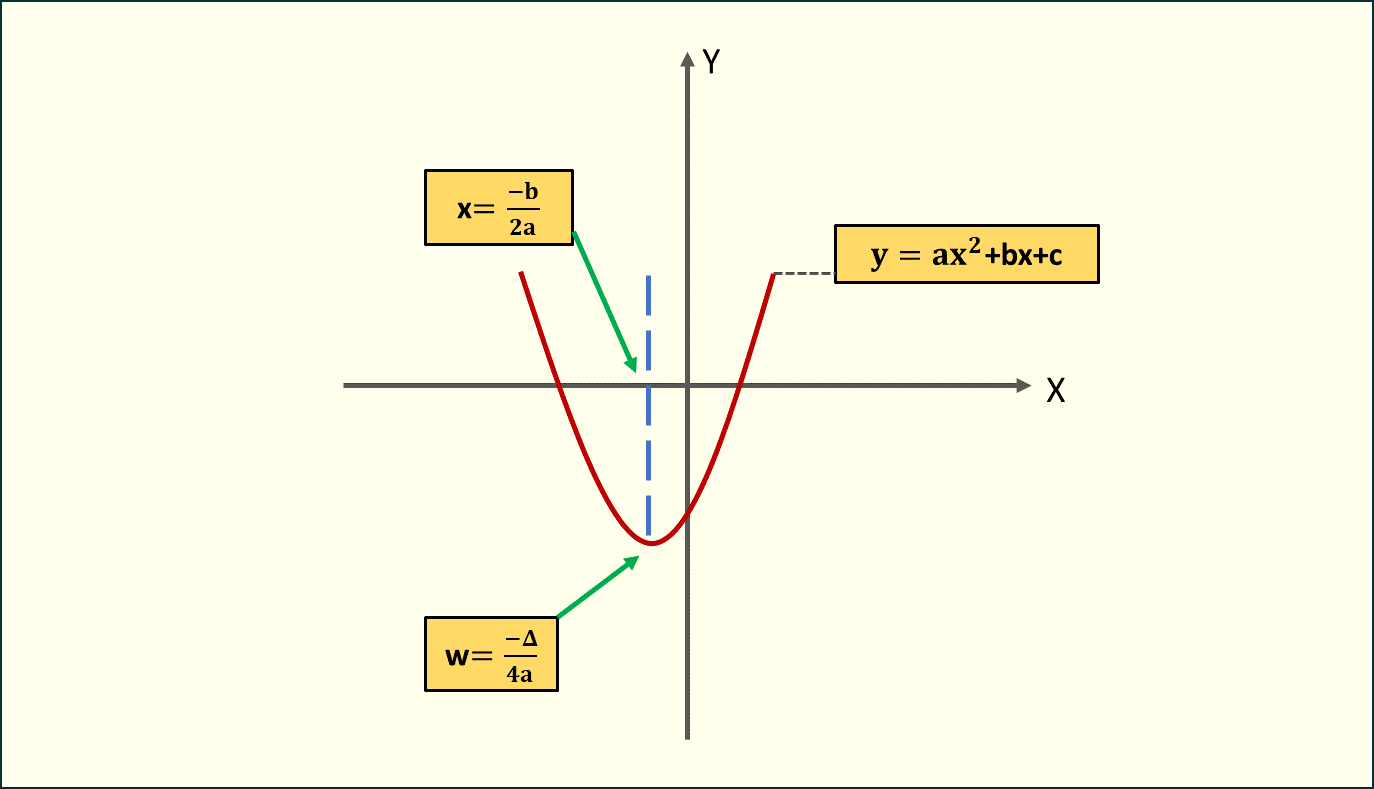
Rys. 4. Położenie minimum funkcji kwadratowej