Koło Mohra na przykładzie
Wprowadzenie
Koło Mohra - graficzna forma rozwinięta przez Christiana Otto Mohra, która obrazuje stan naprężeń głównych i transformację momentów bezwładności przy obrocie układu współrzędnych.
Dane wejściowe do konstrukcji koła Mohra
Aby skonstruować koło Mohra, potrzebujemy następujących danych:
- – kąt głównych centralnych osi bezwładności
- – centralny moment dewiacji układu figur
- , – centralne momenty bezwładności układu figur
- , – główne centralne momenty bezwładności
Elementy do obliczenia
Do konstrukcji koła Mohra należy wyznaczyć:
- – promień koła Mohra
- – środek okręgu (punkt przecięcia osi rzędnych i linii łączącej punkty KL)
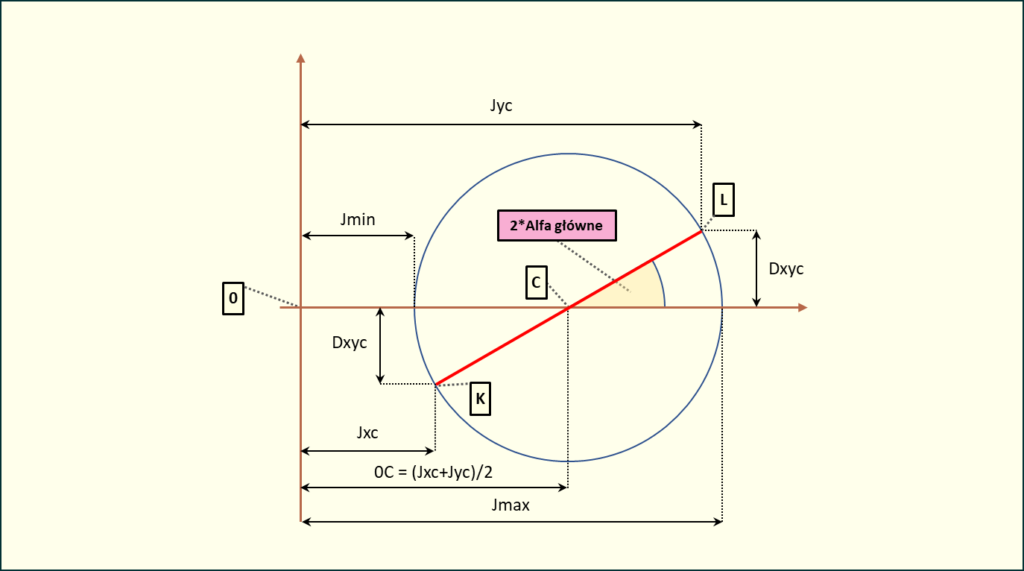
Rys. 1. Schemat koła Mohra z oznaczeniami
Przykład obliczeniowy
Teraz wykonamy obliczenia dla przykładu nr 2 (cały przykład możesz zobaczyć w artykule Momenty bezwładności - przykład nr 2).
Będziemy analizować następujący układ:
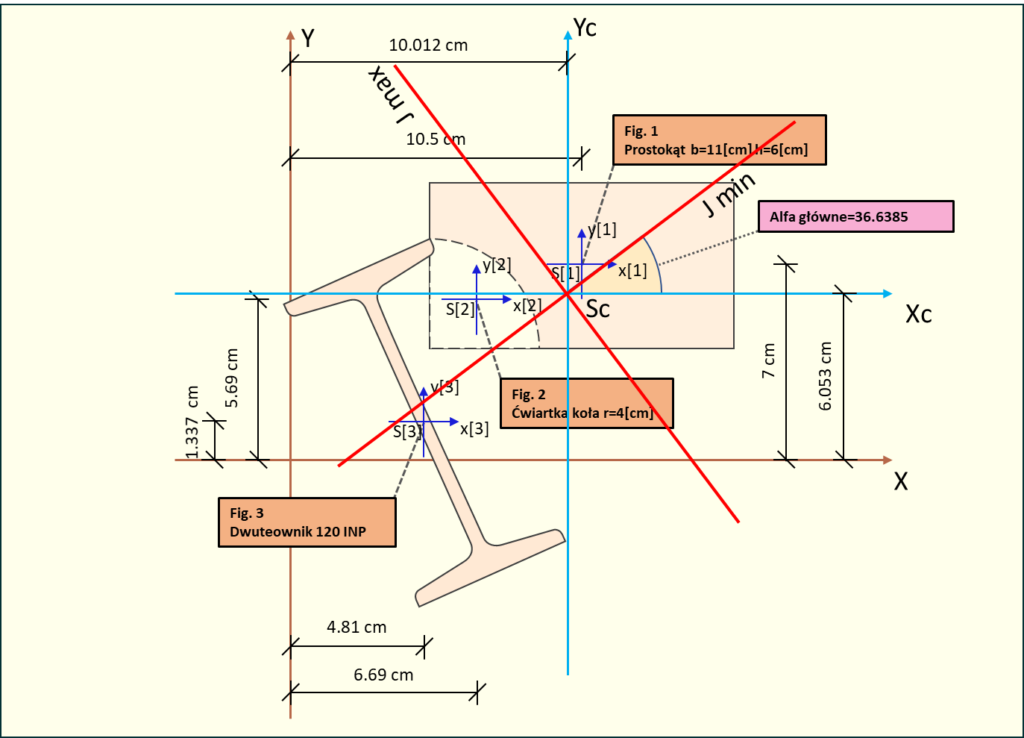
Rys. 2. Układ figur z zaznaczonymi głównymi centralnymi osiami bezwładności
Dane do obliczeń
Z przykładu nr 2 mamy następujące dane:
Obliczenie współrzędnej środka okręgu C
Odkładamy na osi X punkt C w odległości:
Obliczenie promienia koła Mohra
Wzór ogólny na promień:
Podstawiając wartości liczbowe:
Konstrukcja koła Mohra
Z punktu C zakreślamy okrąg o promieniu . Okrąg ten wyznacza na osi X punkty i .
Odkładając na okręgu wartość lub otrzymamy kąt , którego wierzchołkiem jest środek okręgu.
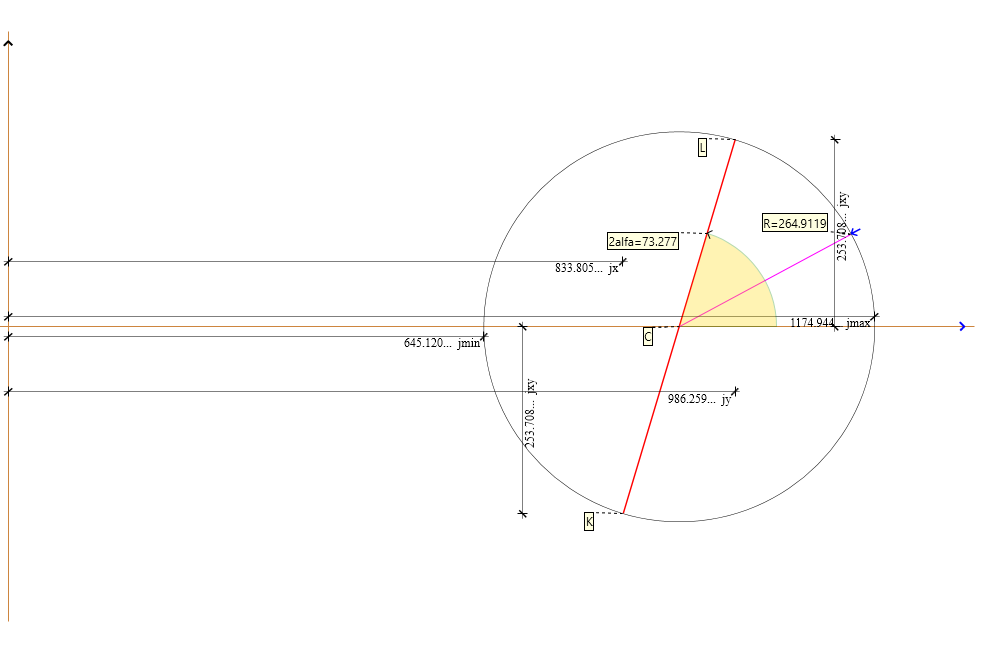
Rys. 3. Koło Mohra
Podsumowanie
Koło Mohra stanowi graficzną interpretację transformacji momentów bezwładności przy obrocie układu współrzędnych. Główne cechy koła Mohra:
- Środek okręgu C leży na osi odciętych w punkcie będącym średnią arytmetyczną momentów i
- Promień okręgu zależy od różnicy momentów bezwładności oraz momentu dewiacji
- Punkty przecięcia z osią X wyznaczają główne momenty bezwładności i
- Kąt na kole Mohra odpowiada kątowi obrotu osi głównych w rzeczywistości
- Koło pozwala odczytać momenty bezwładności i dewiacji dla dowolnego kąta obrotu układu współrzędnych