Kratownica - Metoda Rittera krok po kroku
Zadanie: Dla kratownicy statycznie wyznaczalnej obliczyć siły w prętach Metodą Rittera.
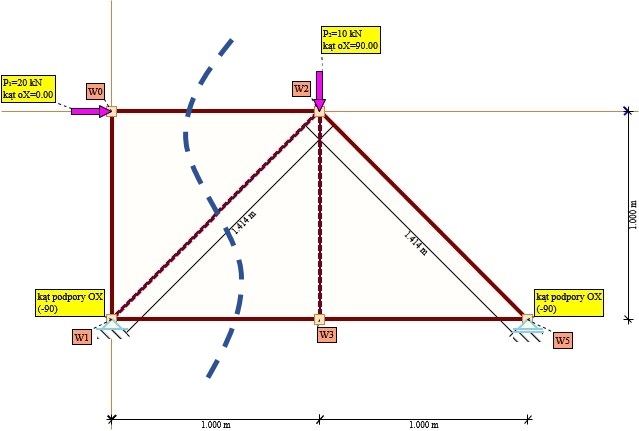
Rys. 1. Schemat kratownicy
1. Obliczanie reakcji podporowych
W tym kroku udajemy się do wpisu Kratownica - metoda równoważenia węzłów.
2. Obliczanie sił w prętach metodą Rittera
Punkt Rittera jest to punkt, w którym przecinają się linie działania pozostałych dwóch sił. W naszym przypadku oznaczono je żółtym prostokątem. Wyliczając Moment Statyczny w Punkcie Rittera od sił i reakcji należących do odciętej części Kratownicy redukujemy w równaniach te niewiadome siły, które się przecinają, ponieważ ramię działania momentu tych sił wynosi zero. Odcięta Kratownica jest w równowadze kiedy suma jej składowych sił i reakcji rzutowana na oś X i oś Y jest równa zero.
gdzie:
- to suma sił odciętej kratownicy rzutowana na oś X
- to suma reakcji podporowych odciętej kratownicy rzutowana na oś X (jeżeli reakcje należą do części)
- to suma odziaływania zewnętrznego odciętej kratownicy rzutowana na oś X (jeżeli siły są przyłożone do części)
- to suma sił prętowych odciętej kratownicy rzutowana na oś Y
- to suma reakcji podporowych odciętej kratownicy rzutowana na oś Y (jeżeli reakcje należą do części)
- to suma odziaływania zewnętrznego odciętej kratownicy rzutowana na oś Y (jeżeli siły są przyłożone do części)
3. Wybrano Przecięcie = 0
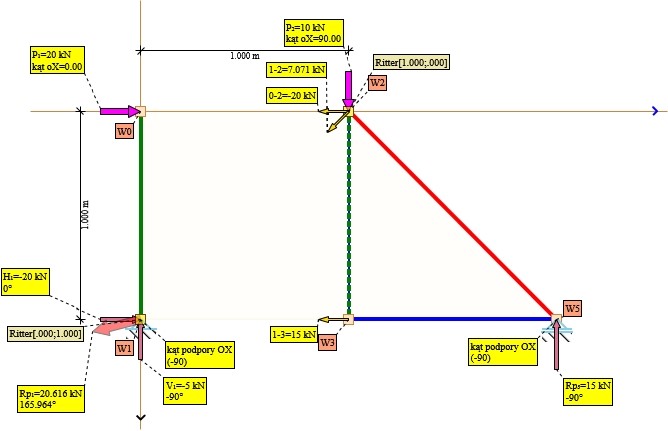
Rys. 2. Przekrój kratownicy - przecięcie 0
W tym przypadku są dwa punkty Rittera i do policzenia sił należy rozwiązać układ równań:
- Suma Momentu Statycznego względem punktu Rittera
- Rzutując niewiadome siły oraz oddziaływania P na oś X
- Rzutując niewiadome siły oddziaływania P na oś Y
Oczywiste jest, że wyznaczenie siły w pręcie nie przecinającym się w punkcie Rittera jest natychmiastowe ponieważ tylko ta siła tworzy równanie z jedną niewiadomą.
Do policzenia: ,
Do policzenia: ,
Do policzenia: ,
3.1. Moment względem Punktu Rittera [0;1]
3.2. Moment względem Punktu Rittera [1;0]
3.3. Moment względem Punktu Rittera [0;0]
3.4. Rzutowanie na oś X
3.5. Rzutowanie na oś Y
Wyliczono:
4. Wybrano Przecięcie = 1
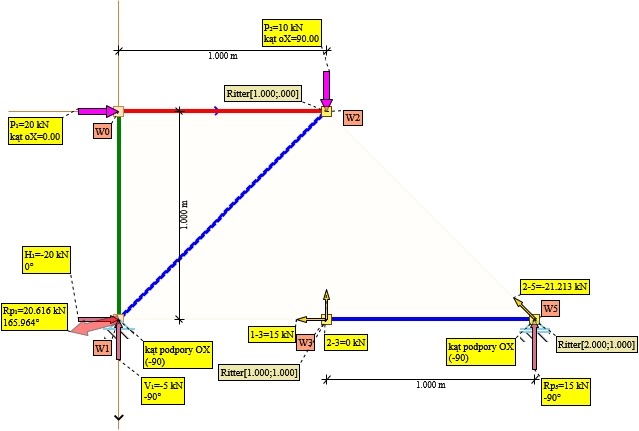
Rys. 3. Przekrój kratownicy - przecięcie 1
W tym przypadku są trzy punkty Rittera i do policzenia sił należy rozwiązać pojedyncze równanie:
- Suma Momentu Statycznego względem punktu Rittera nr 1
- Suma Momentu Statycznego względem punktu Rittera nr 2
- Suma Momentu Statycznego względem punktu Rittera nr 3
Oczywiste jest że wyznaczenie siły w pręcie nie przecinającym się w punkcie Rittera jest natychmiastowe ponieważ tylko ta siła tworzy równanie z jedną niewiadomą.
Wygodnie jest policzyć od razu ramię działania siły nieznanej ze wzoru na przekątną trójkąta prostokątnego, gdzie bokami trójkąta są różnice współrzędnych X i Y pomiędzy Punktem Rittera a danym punktem siły szukanej.
I jeżeli siła prętowa nie działa pod kątem prostym to cosinus kąta działania siły jest pomiędzy prętem a rzutem prostopadłym na kierunek prostej ramienia.
Oczywiście można również obliczyć moment tej siły obliczając jej składowe względem osi X i względem osi Y.
Do policzenia: ,
Do policzenia: ,
Do policzenia: ,