Metoda Sił - podejście Maxwella-Mohra
Wprowadzenie
Metoda sił - metoda służąca do rozwiązywania układów statycznie niewyznaczalnych (belek, ram, kratownic).
Co to są układy statycznie niewyznaczalne, możesz dowiedzieć się w artykule Konstrukcje statycznie niewyznaczalne.
Algorytm obliczeń
- Ustalanie stopnia statycznej niewyznaczalności układu
- Przyjęcie układu podstawowego i układu równań metody sił
- Obliczanie układu podstawowego dla sił wirtualnych X
- Obliczanie współczynników macierzy sztywności
- Obliczanie układu podstawowego dla stanu P
- Współczynniki wyrazów wolnych
- Macierz współczynników i wyrazów wolnych
- Obliczanie i sprawdzenie reakcji podporowych
- Obliczanie momentów przywęzłowych, sił tnących, sił normalnych
Przykład obliczeniowy
Zadanie: Wyznaczyć wykresy M, T, N dla ramy przedstawionej na poniższym schemacie przy pomocy metody sił.
1. Schemat zadania
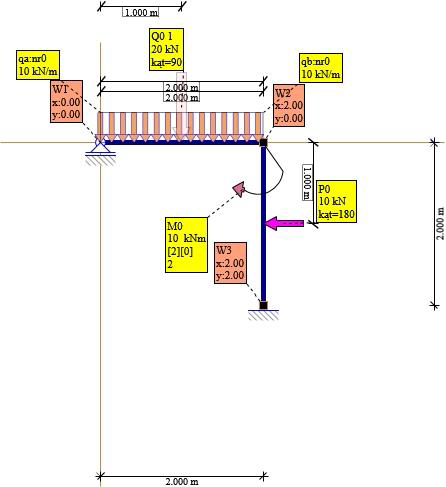
Rys. 1. Schemat układu
Przyjęto przekrój podstawowy:
- I = 3060 cm⁴
- E = 205 GPa
- Globalne EI = 6273 kNm²
- Globalne EA = 809750 kN
2. Ustalenie stopnia statycznej niewyznaczalności układu (SSN)
- Liczba tarcz: T = 1
- Więzi podporowe: P = 4
- Przeguby sprowadzone: węzłowe R₀ = 0, dołączone R₁ = 0
- Pola zamknięte sprowadzone: Pz = 3·(0-1) = -3
- Połączenie wewnętrzne teleskopowe typu łyżwa: Stł = 0
- Połączenie wewnętrzne teleskopowe typu tuleja: Stt = 0
Wzór ogólny:
Układ jest 1-krotnie statycznie niewyznaczalny (1 nadliczbowe).
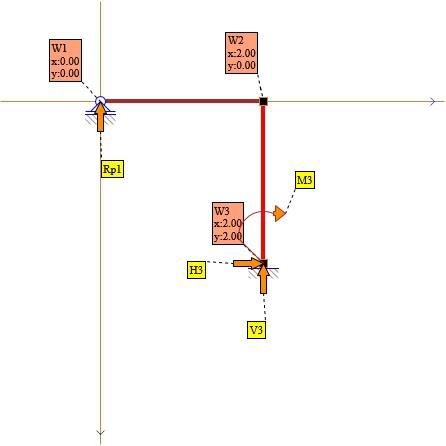
Rys. 2. Reakcje układu do policzenia
Współrzędne węzłów:
- Węzeł 1: x = 0.000 m, y = 0.000 m
- Węzeł 2: x = 2.000 m, y = 0.000 m
- Węzeł 3: x = 2.000 m, y = 2.000 m
3. Przyjęcie układu podstawowego
Aby dany układ był statycznie wyznaczalny, należy zastąpić 1 nieznane nadliczbowe siłami zastępczymi X. Powstały układ podstawowy musi jednak spełniać warunek geometrycznej niezmienności.
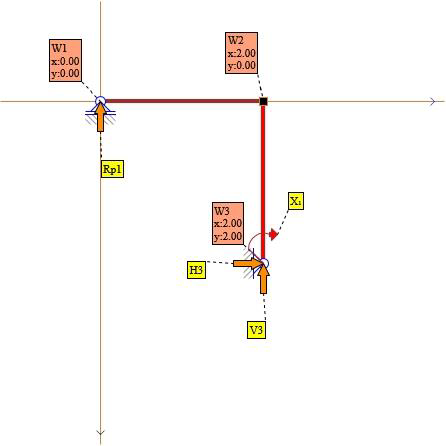
Rys. 3. Układ podstawowy metody sił
Układ równań metody sił dla układu podstawowego:
4. Obliczenie układu podstawowego dla X₁
Działa tylko X₁.
Sprawdzono poprawność obliczeń dla schematu statycznego.
Pręt 1-2: Mik = 0, Mki = 1
Pręt 2-3: Mik = (-1), Mki = 1
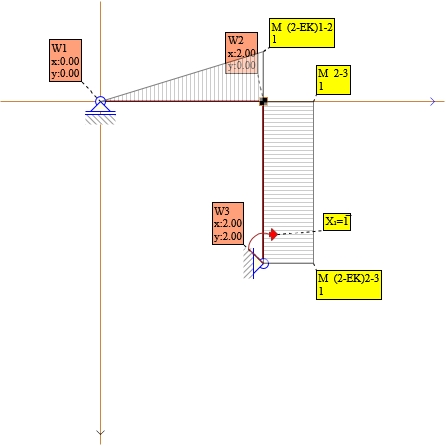
Rys. 4. Momenty dla X1
5. Obliczenie współczynników macierzy sztywności
Dla prętów o osiach prostych i stałym EI, EA, GA do obliczania współczynników można stosować: wzór Mohra (Wereszczagina) ,wzór trapezów, wzór Simpsona lub inne. Gotowe wzory Wereszczagina czy wzór Simpsona można stosować dla przypadków z ograniczeniami. Najbardziej uniwersalnym i bez ograniczeń jest wzór Mohra z wersją całkowania przebiegu funkcji wykresu. Określenie przebiegu funkcji wykresu przy znanym obciążeniu nie jest problemem. Środek ciężkości i pole obliczymy wtedy poprzez całkowanie. Mając Pole wykresu, środek ciężkości i funkcje przebiegu wykresu bezproblemowo zastosujemy:∫F(x) f(x)dx = ΩF f(xc) , ΩF - pole wykresu funkcji F(x) w przedziale całkowania, f(xc) - wartość funkcji f(x) w punkcie xc , w którym znajduje się środek ciężkości funkcji F(x).
Gdzie:
- - współrzędna środka ciężkości
- - moment statyczny względem osi
- - pole powierzchni wykresu z osią OX
Obliczenia Całek dołączono osobnym zbiorem do projektu. Metodę liczenia przyjęto w zależności od wybranej opcji sposobu liczenia.
6. Obliczenie współczynników X
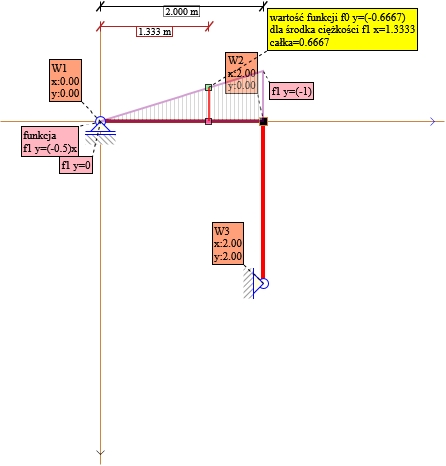
Rys. 5. Składnik nr 1 X1 X1
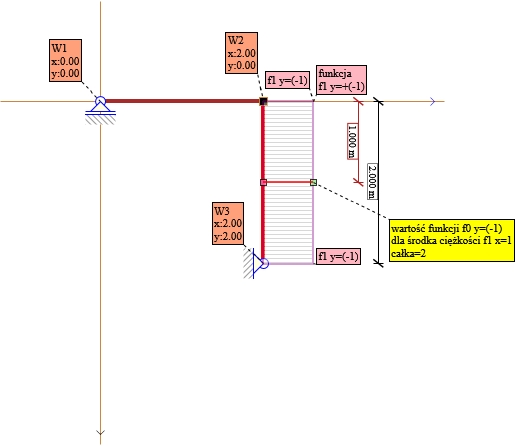
Rys. 6. Składnik nr 2 X1 X1
7. Współczynniki Macierzy Sztywności
Składnik M nadliczbowa
Macierz sztywności bez podzielenia przez EI, EA, GA
8. Obliczenie układu podstawowego dla Stan P
W celu ułatwienia całkowania układ obciążamy kolejno poszczególnymi obciążeniami stanu P
działa tylko P0, sprawdzono poprawność obliczeń dla schematu statycznego
Pręt 1-2 Mik=0 , Mki=(-10) kNm
Pręt 2-3 Mik=10 , Mki=0 kNm
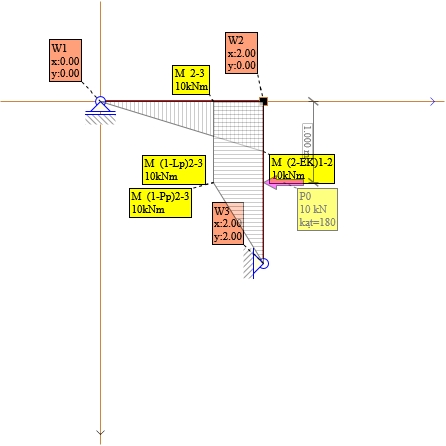
Rys. 7. Momenty dla P0
działa tylko q0, sprawdzono poprawność obliczeń dla schematu statycznego
Pręt 1-2 Mik=0 , Mki=0 kNm
Pręt 2-3 Mik=0 , Mki=0 kNm
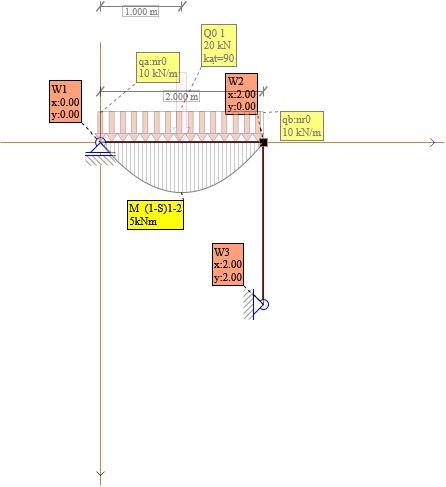
Rys. 8. Momenty dla q0
działa tylko M0, sprawdzono poprawność obliczeń dla schematu statycznego
Pręt 1-2 Mik=0 , Mki=10 kNm
Pręt 2-3 Mik=0 , Mki=0 kNm
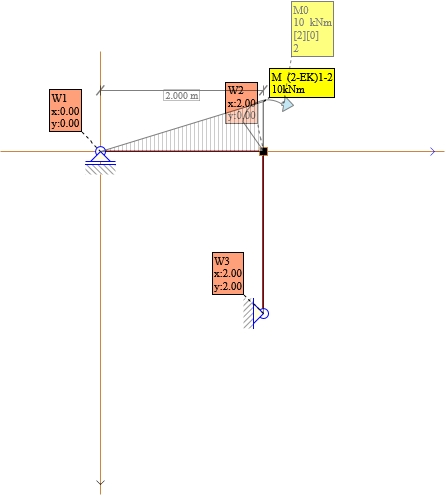
Rys. 9. Momenty dla M0
działa tylko SilosAll, sprawdzono poprawność obliczeń dla schematu statycznego
Pręt 1-2 Mik=0 , Mki=6.875 kNm
Pręt 2-3 Mik=3.125 , Mki=6.875 kNm
9. Obliczenie współczynników obciążenia
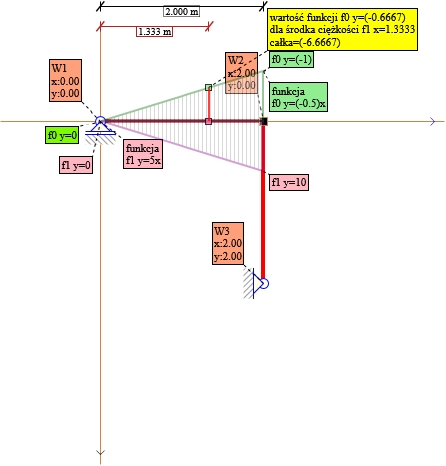
Rys. 10. Składnik nr 3 X1 P0
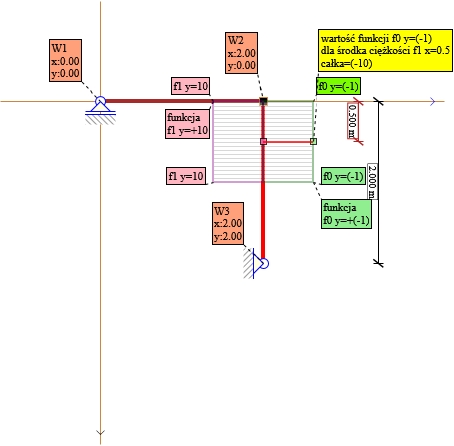
Rys. 11. Składnik nr 4 X1 P0
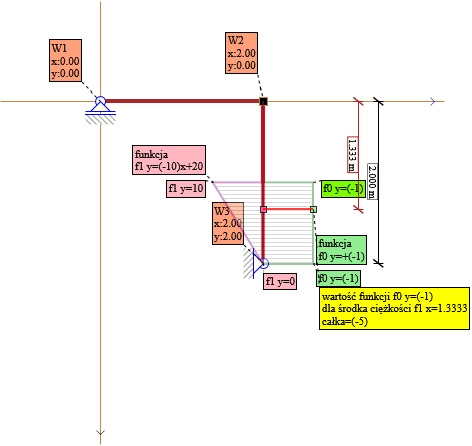
Rys. 12. Składnik nr 5 X1 P0
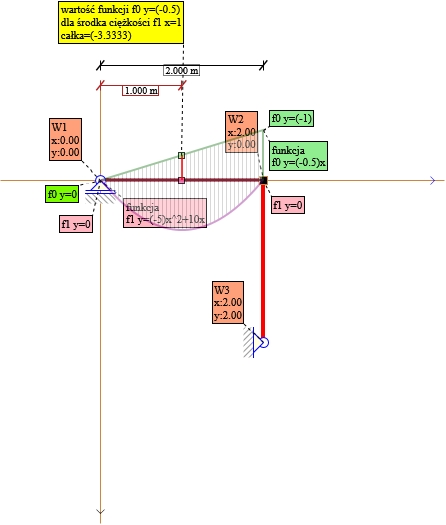
Rys. 13. Składnik nr 6 X1 P0
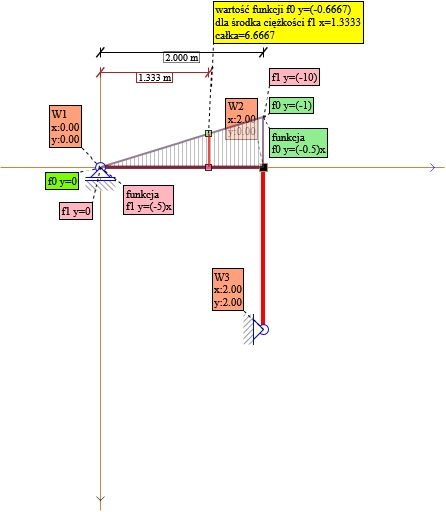
Rys. 14. Składnik nr 7 X1 P0
10. Współczynniki Wyrazów Wolnych
Składnik M obciążenie:
Wyrazy Wolne
11. Macierz Współczynników i Wyrazów Wolnych
Składnik M nadliczbowa:
Składnik M obciążenie:
Układ równań kanonicznych materiałowy:
Po rozwiązaniu układu otrzymano:
12. Obliczenie MTN dla wszystkich działających i obliczonych oddziaływań
Obciążamy układ podstawowy obliczonymi reakcjami nadliczbowymi oraz obciążeniem istniejącym
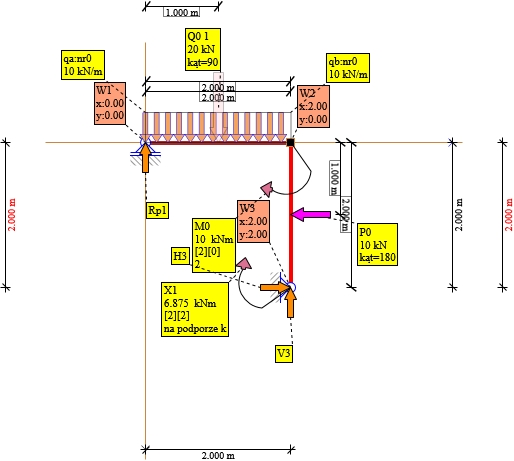
Rys. 15. Układ podstawowy do policzenia
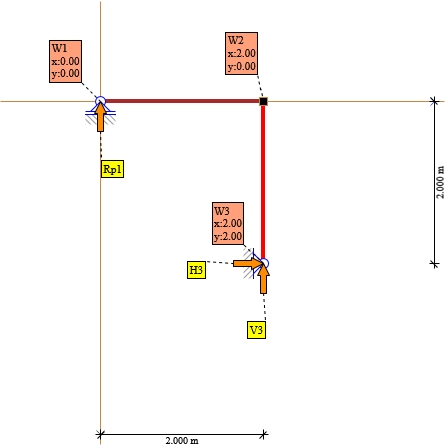
Rys. 16. Reakcje układu podstawowego do policzenia
Składniki układu równań dla sumy X:
Składniki układu równań dla sumy Y:
Składniki układu równań dla sumy M w punkcie [0;0]:
Układ równań:
Po rozwiązaniu układu otrzymano:
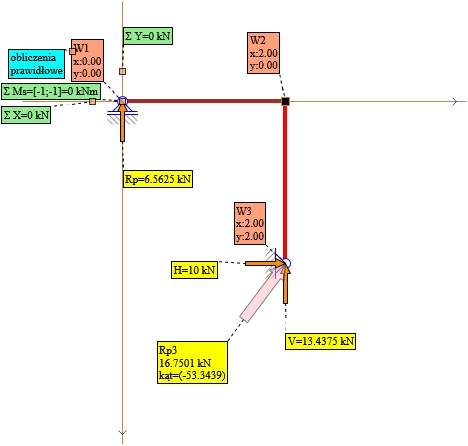
Rys. 17. Reakcje podporowe obliczone
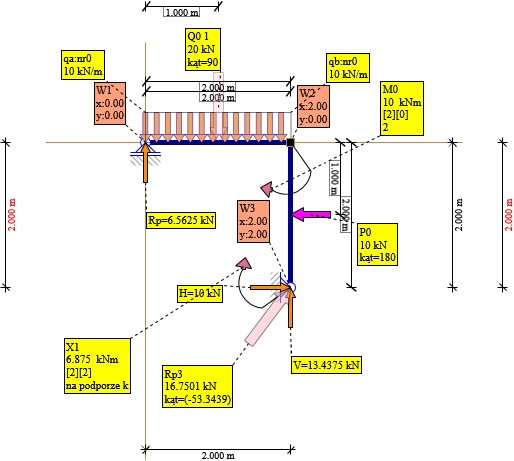
Rys. 18. Reakcje do sprawdzenia MXY
13. Sprawdzenie Reakcji Podporowych Moment
Sprawdzenia poprawności wyznaczenia reakcji podporowych dokonamy w punkcie [(-1); (-1)] układzie XY. Punkt musi być tak dobrany, aby wszystkie siły i reakcje brały udział w obliczaniu Sumy Momentów. W punkcie tym Suma Momentów od wszystkich sił i reakcji powinna wynosić M=0.
14. Sprawdzenie Reakcji Podporowych Rzut X
15. Sprawdzenie Reakcji Podporowych Rzut Y
16. Ocena Wyników Obliczeń
Z uwagi na spełnione warunki:
Ocena: obliczenia prawidłowe
17. Obliczenie Momentów przywęzłowych
Pręt 1-2 Mik=0 , Mki=6.875 kNm
Pręt 2-3 Mik=3.125 , Mki=6.875 kNm
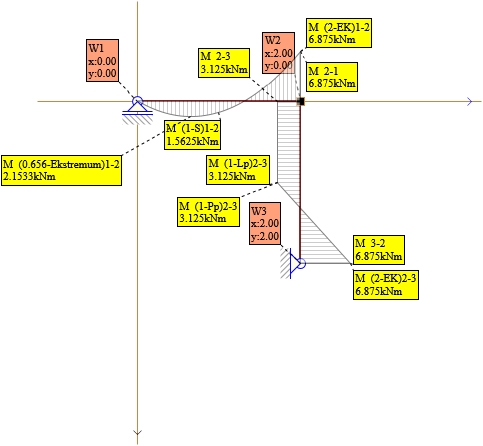
Rys. 19. Wykresy M wszystkie
18. Obliczenie Sił Tnących
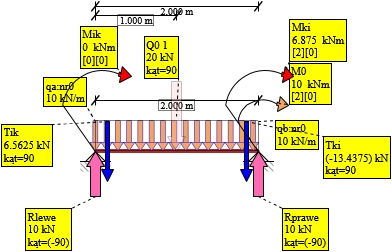
Rys. 20. Siły Tnące 1-2
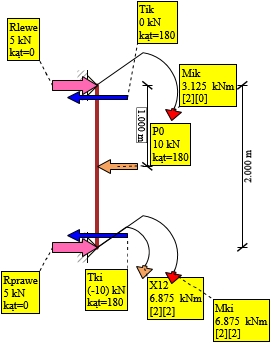
Rys. 21. Siły Tnące 2-3
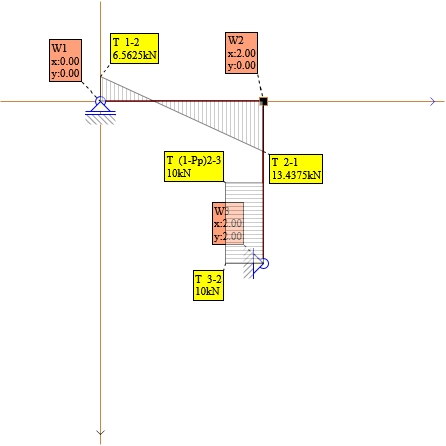
Rys. 22. Wykresy T wszystkie
19. Obliczenie sił Normalnych
Aby Węzeł był w równowadze to suma jego składowych sił i reakcji rzutowana na oś X i oś Y musi być równa zero:
Gdzie:
- to suma sił prętowych rzutowana na oś X w Węźle
- to suma reakcji podporowych rzutowana na oś X w Węźle - jeżeli istnieją
- to suma oddziaływania zewnętrznego rzutowana na oś X w Węźle - jeżeli jest przyłożona
- to suma sił prętowych rzutowana na oś Y w Węźle
- to suma reakcji podporowych rzutowana na oś Y w Węźle - jeżeli istnieją
- to suma oddziaływania zewnętrznego rzutowana na oś Y w Węźle - jeżeli jest przyłożona
Obliczenia rozpoczynamy od Węzła, dla którego liczba niewiadomych sił w Prętach jest ≤2.
Elementy szukane oznaczono kolorem czerwonym. Elementy zerowe są przedstawione w tle rysunku.
Wybrano Węzeł = 1
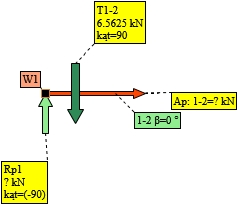
Rys. 23. Węzeł 1
Do policzenia
Rzutowanie na oś X:
Rzutowanie na oś Y:
Równanie X:
Równanie Y:
Wybrano Węzeł = 2
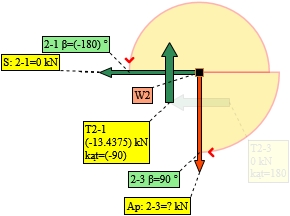
Rys. 24. Węzeł 2
Do policzenia
policzone
Rzutowanie na oś X:
Rzutowanie na oś Y:
Równanie X:
Równanie Y:
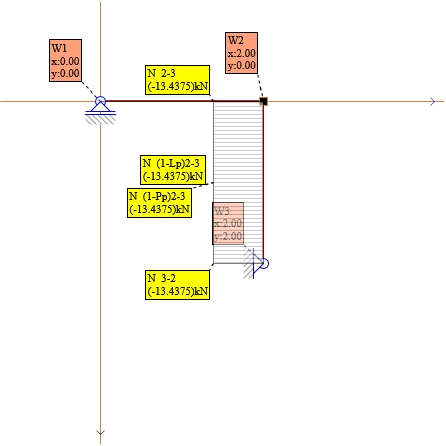
Rys. 25. Wykresy N wszystkie
20. Sprawdzenie Kinematyczne
Sprawdzamy czy przemieszczenia w poszczególnych punktach spełniają warunki podparcia i ciągłości. Wystarczy sprawdzić tyle składowych ile wynosi SSN (Stopień Statycznej Niewyznaczalności). Przekształcamy schemat naszego układu na statycznie wyznaczalny poprzez redukcje Nadliczbowych więzów. W miejscach usuniętych nadliczbowych przykładamy kolejno obciążenia jednostkowe i wyznaczamy momenty zginające. Obciążenia jednostkowe dla kątów obrotu mają charakter momentów jednostkowych. Obciążenia jednostkowe dla przemieszczeń liniowych charakter sił jednostkowych. Przemieszczenia wynikowe obliczamy ze wzoru Maxwella-Mohra
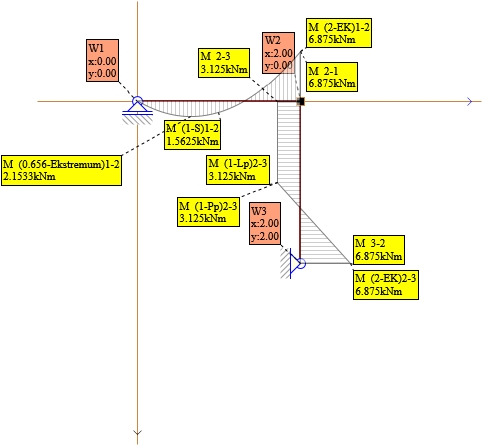
Rys. 26. Wykresy M wszystkie
21. Obliczenie układu podstawowego dla X1
Działa tylko X1.
Sprawdzono poprawność obliczeń dla schematu statycznego.
Pręt 1-2 Mik=0 , Mki=1
Pręt 2-3 Mik=(-1) , Mki=1
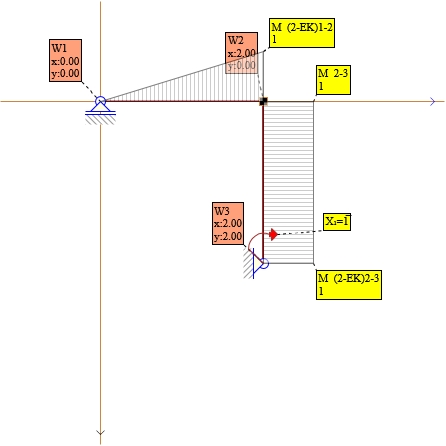
Rys. 27. Momenty dla X1
22. Obliczenie współczynników obciążenia
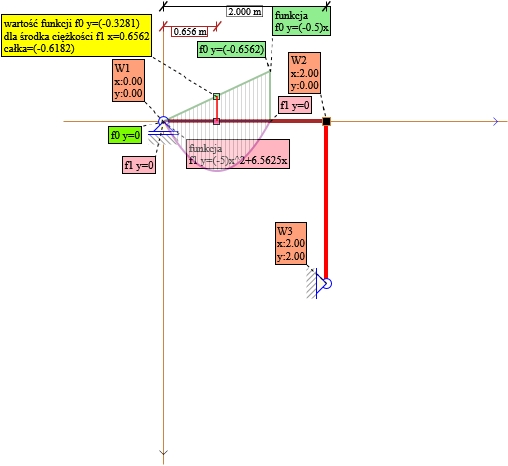
Rys. 28. Składnik nr8 X1 wszystkie
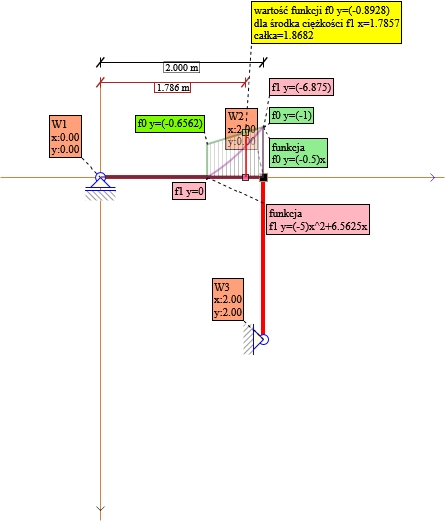
Rys. 29. Składnik nr9 X1 wszystkie
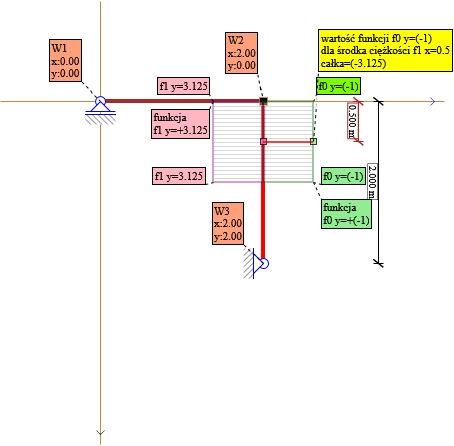
Rys. 30. Składnik nr10 X1 wszystkie
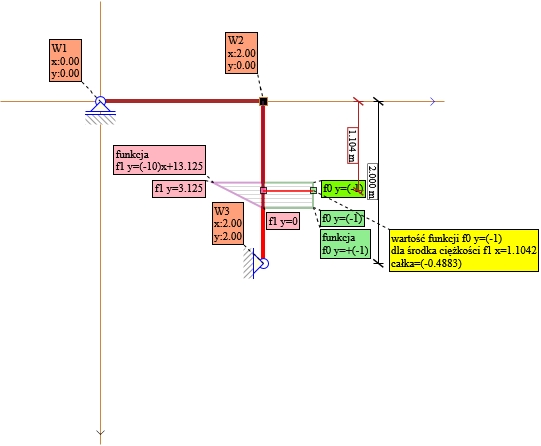
Rys. 31. Składnik nr11 X1 wszystkie
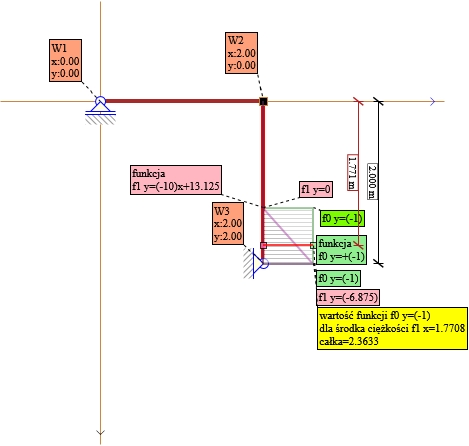
Rys. 32. Składnik nr12 X1 wszystkie
23. Suma Współczynników Kontrolnych
Składnik M obciążenie:
Suma współczynników pomiarowych:
[0]
Obliczenia dokonane w programie Silos.