Momenty bezwładności - przykład nr 2
Wprowadzenie
Zadanie: Wyznaczyć położenie głównych centralnych osi bezwładności i obliczyć główne centralne momenty bezwładności dla układu składającego się z prostokąta, ćwiartki koła oraz dwuteownika.
1. Schemat zadania
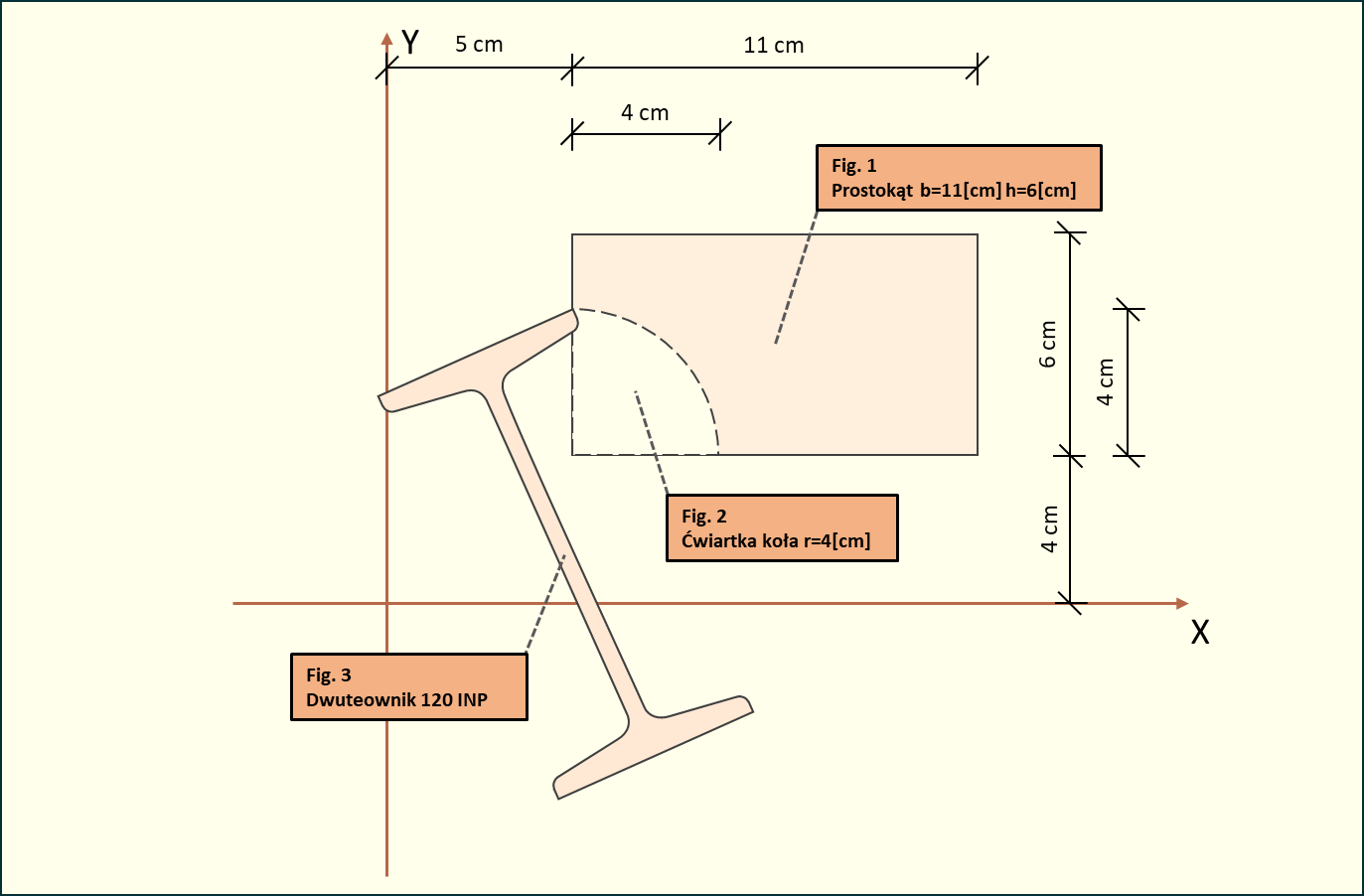
Rys. 1. Schemat układu dla przykładu nr 2
2. Oznaczenia
Podstawowe oznaczenia używane w obliczeniach:
- – numer figury, gdzie
- – pole powierzchni figury
- – współrzędna X środka ciężkości figury w układzie globalnym
- – współrzędna Y środka ciężkości figury w układzie globalnym
- – współrzędne środka ciężkości figury
- – moment statyczny względem osi Y w układzie globalnym
- – moment statyczny względem osi X w układzie globalnym
- – współrzędna X środka ciężkości układu figur
- – współrzędna Y środka ciężkości układu figur
- – odległość w osi X pomiędzy środkiem ciężkości figury a środkiem ciężkości całego układu
- – odległość w osi Y pomiędzy środkiem ciężkości figury a środkiem ciężkości całego układu
- – moment bezwładności figury względem osi X
- – moment bezwładności figury względem osi Y
- – dewiacyjny moment bezwładności figury
- […tablice] – wartość odczytana z Tablic Inżynierskich
3. Transformacje geometryczne
3.1. Transformacja kątowa
Współrzędne i po obrocie układu wyznacza się ze wzorów:
gdzie są współrzędnymi po transformacji kątowej, współrzędnymi przed transformacją, a jest kątem obrotu układu względem układu (ujemnym przy obrocie zgodnym z ruchem wskazówek zegara).
3.2. Transformacja liniowa
Współrzędne i po przesunięciu układu wyznacza się ze wzorów:
gdzie i oznaczają współrzędne nowego początku układu.
4. Charakterystyki geometryczne poszczególnych figur układu
Obliczenie nowych wartości środka ciężkości figury po obrocie o kąt i przesunięciu do punktu docelowego. Figura znajduje się teraz w takim położeniu jak wzory podane na obliczanie momentów. Układ taki nazywamy układem lokalnym figury.
4.1. Figura nr 1 - Prostokąt
- kąt
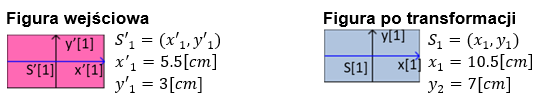
Rys. 2. Figura nr 1 - prostokąt przed i po transformacji
Transformacja liniowa figury do punktu docelowego o wektor i :
Pole powierzchni i momenty statyczne:
Wartości , , w układzie bez obrotu figury:
4.1.1. Układ nachylony
Kąt nachylenia jest równy zero względem układu XY, więc układ nachylony nie występuje.
4.1.2. Ocena znaku figury
Pole dodatnie - figura została podana jako dodatnia. Wartości , , zachowują swoje znaki.
4.2. Figura nr 2 - Ćwiartka koła
- kąt
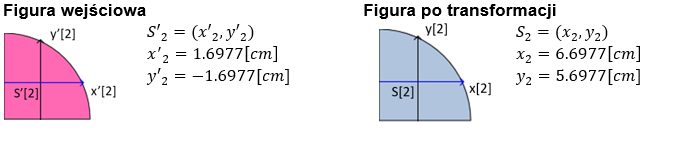
Rys. 3. Figura nr 2 - ćwiartka koła przed i po transformacji
Transformacja liniowa figury do punktu docelowego o wektor i :
Wartości , , w układzie bez obrotu figury:
4.2.1. Układ nachylony
Kąt nachylenia jest równy zero względem układu XY, więc układ nachylony nie występuje.
4.2.2. Ocena znaku figury
Pole ujemne - figura została podana jako ujemna. Wartość (pole powierzchni) zostało zmienione na ujemne.
Wartości momentów bezwładności zmieniają znaki:
4.3. Figura nr 3 - Dwuteownik 120 INP
- kąt
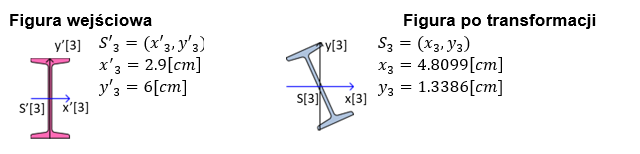
Rys. 4. Figura nr 3 - dwuteownik w układzie lokalnym
Transformacja kątowa figury w układzie lokalnym o kąt:
Obliczenie współrzędnych po transformacji kątowej:
Transformacja liniowa figury do punktu docelowego o wektor i :
Wartości , , w układzie bez obrotu figury (odczytane z tablic):
4.3.1. Momenty i dewiacje dla układu nachylonego
Ponieważ kąt nachylenia analizowanej figury jest różny od zera i wynosi , należy obliczyć układ nachylony.
4.3.2. Jx₃ w układzie nachylonym
4.3.3. Jy₃ w układzie nachylonym
4.3.4. Dxy₃ w układzie nachylonym
4.3.5. Ocena znaku figury
Pole dodatnie - figura została podana jako dodatnia. Wartości , , zachowują swoje znaki.
5. Środki ciężkości figur w układzie
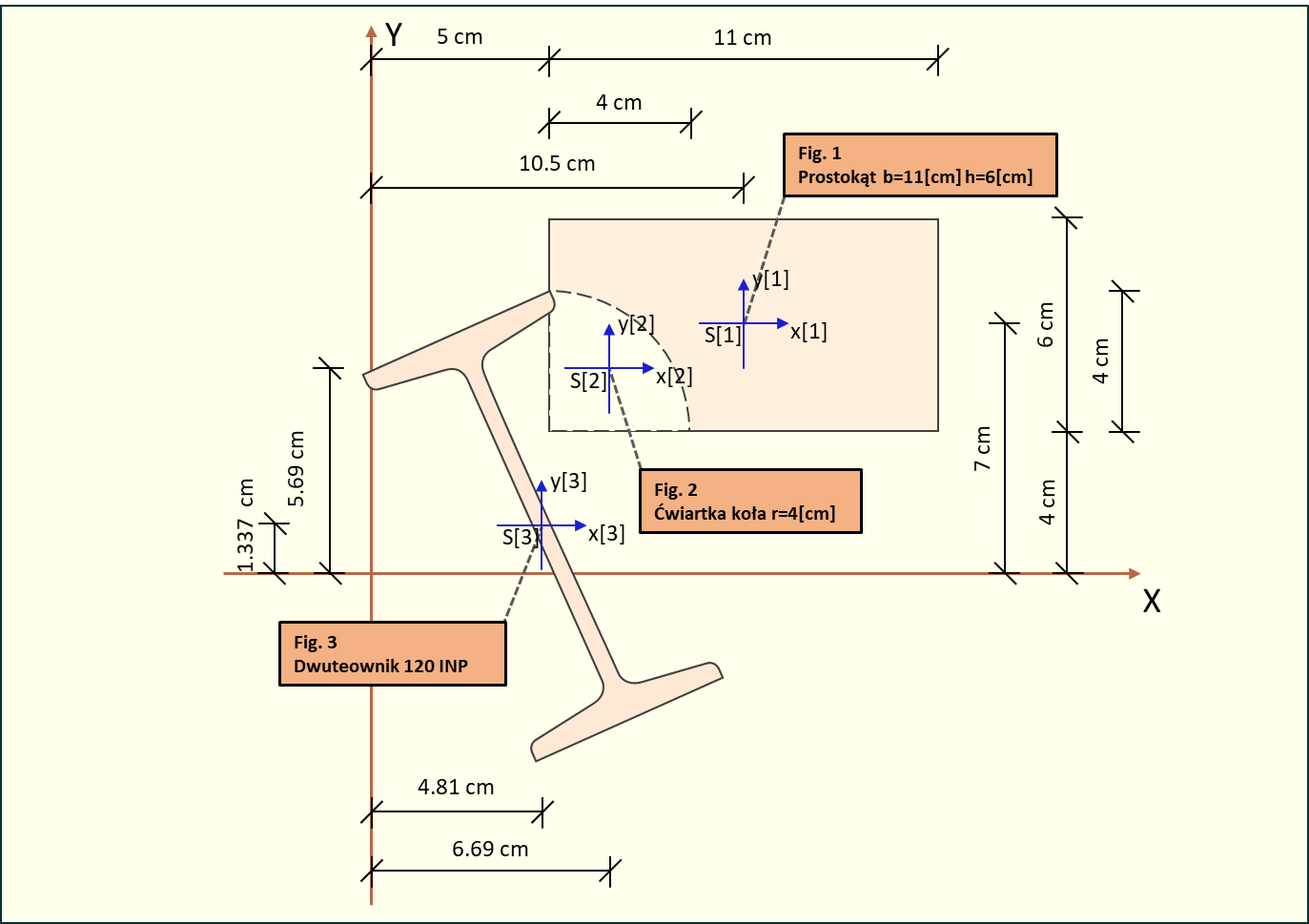
Rys. 5. Środki ciężkości poszczególnych figur w układzie globalnym
6. Położenie głównych centralnych osi bezwładności (xc, yc) względem układu XY
Dla ułatwienia obliczeń zestawimy wszystkie dane w formie tabelarycznej:

Tab. 1. Zestawienie charakterystyk poszczególnych figur
Obliczenie środka ciężkości układu:
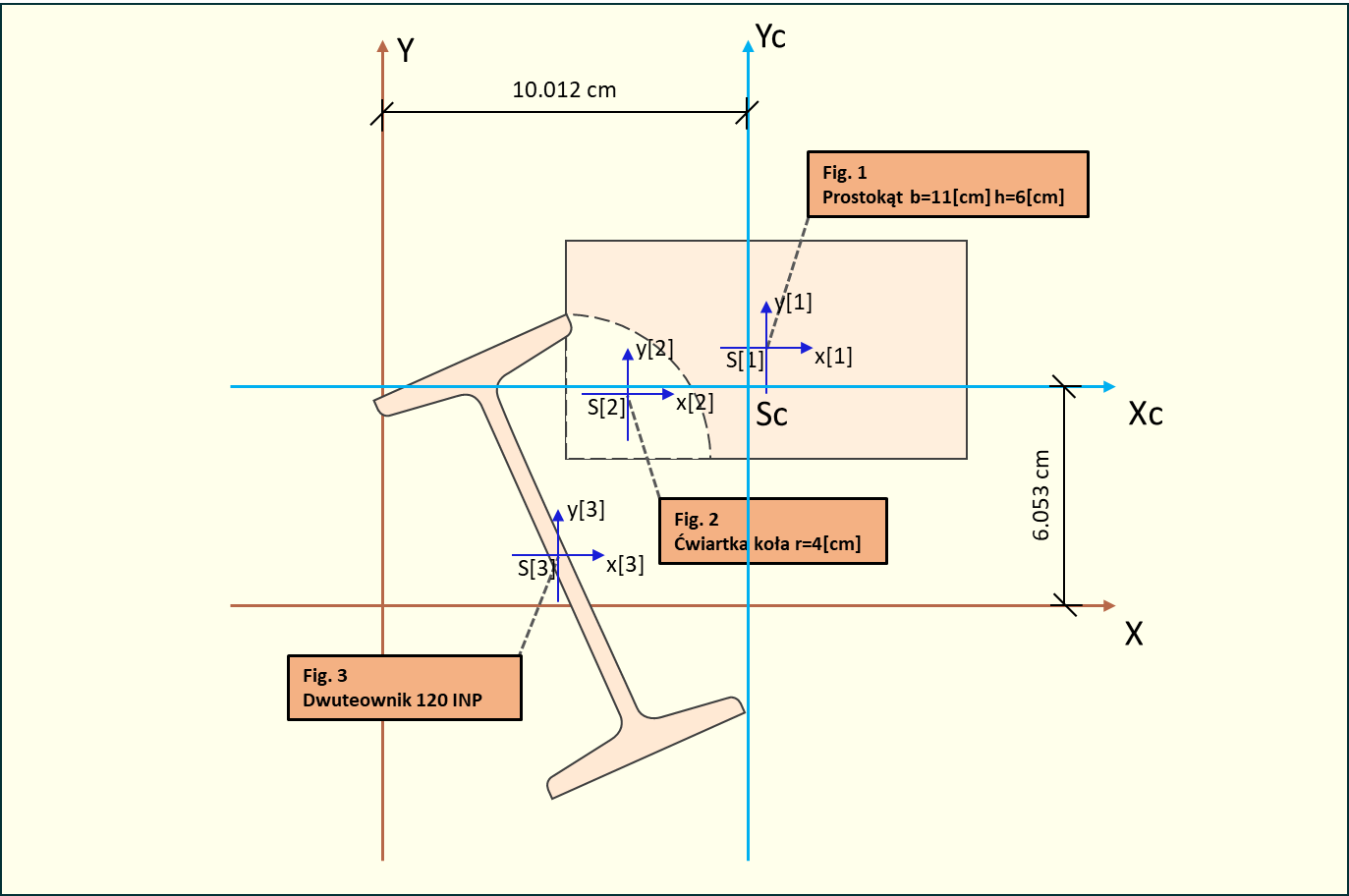
Rys. 6. Główne centralne osie bezwładności
7. Odległości od środka ciężkości figury do środka ciężkości układu
Wzory ogólne:
7.1. Figura nr 1 - Prostokąt
Prostokąt cm, cm:
7.2. Figura nr 2 - Ćwiartka koła
Ćwiartka koła cm:
7.3. Figura nr 3 - Dwuteownik 120 INP
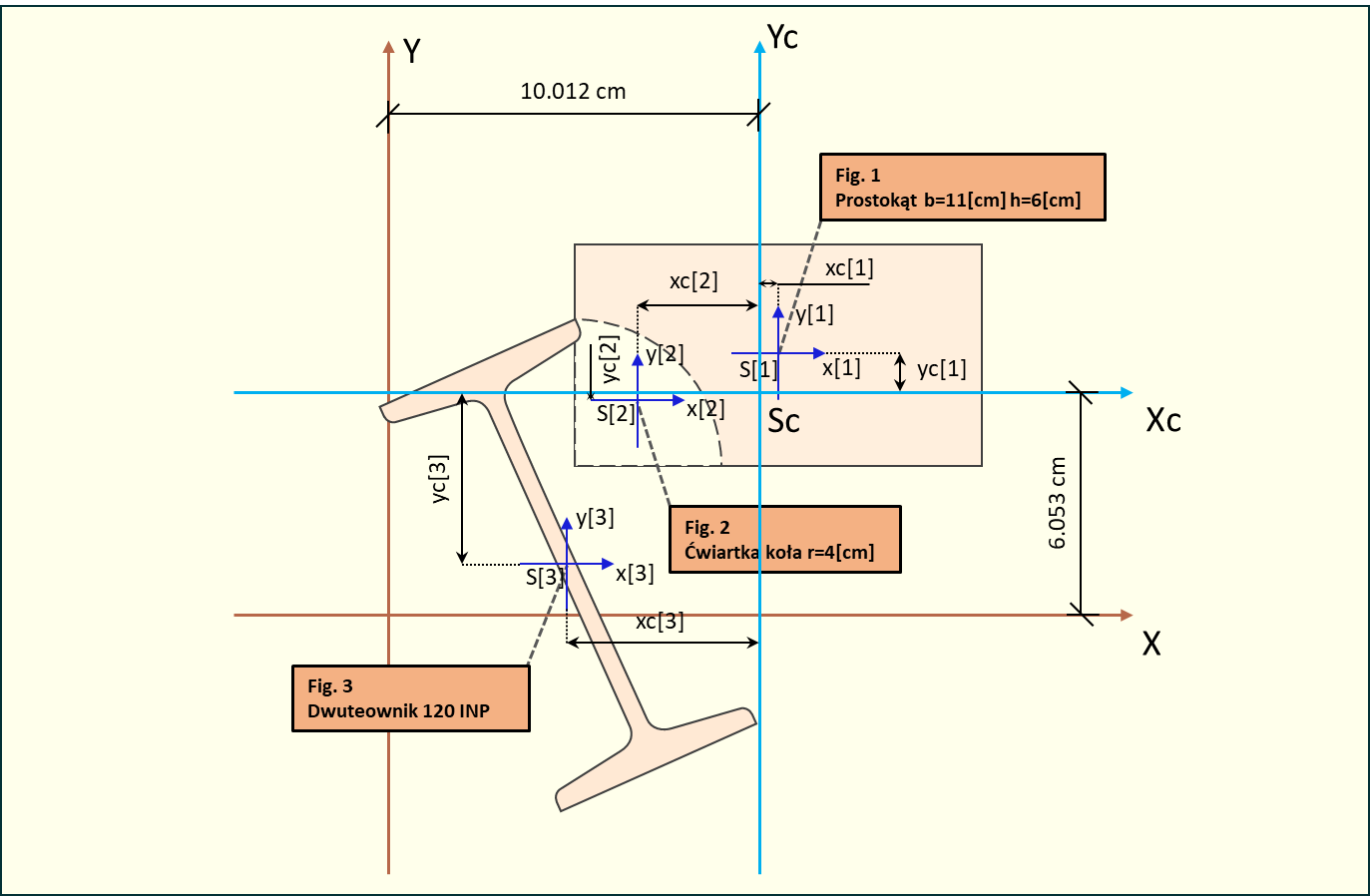
Rys. 7. Odległości środków ciężkości poszczególnych figur do środka ciężkości układu
8. Centralne momenty bezwładności dla układu xc, yc
Zestawienie wszystkich danych potrzebnych do obliczenia centralnych momentów bezwładności:

Tab. 2. Zestawienie momentów i dewiacji poszczególnych figur
8.1. Sumy częściowe
8.2. Elementy do wzoru Steinera
9. Momenty bezwładności całego układu (twierdzenie Steinera)
To są centralne momenty bezwładności układu figur obliczone zgodnie z twierdzeniem Steinera.
10. Kąt alfa głównych centralnych osi bezwładności
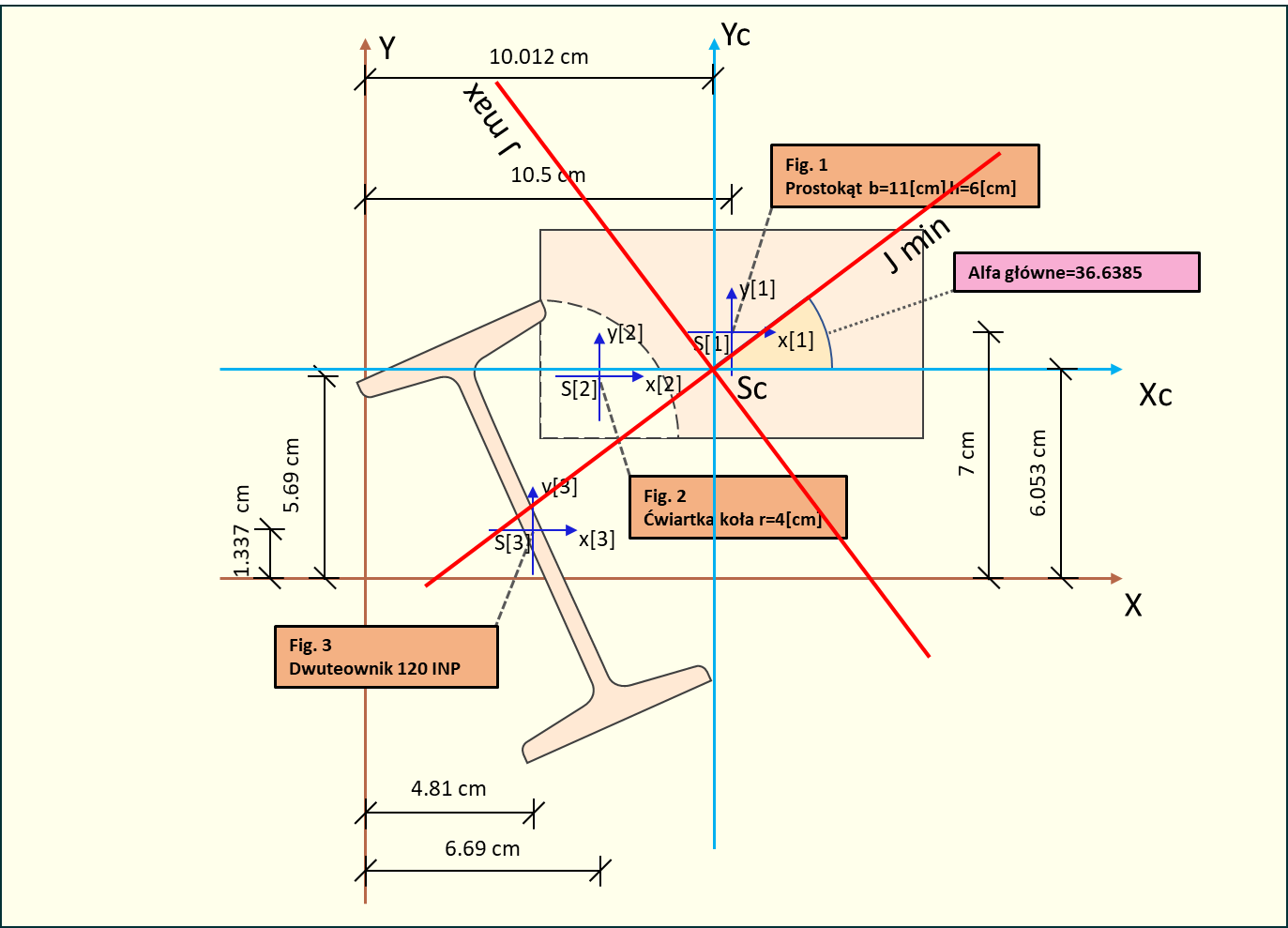
Rys. 8. Kąt alfa głównych centralnych osi bezwładności - rysunek końcowy
11. Główne centralne momenty bezwładności
11.1. Jmax
11.2. Jmin
12. Sprawdzenie
12.1. Niezmiennik J₁
12.2. Niezmiennik J₂
13. Momenty bezwładności dla układu XY w punkcie [0,0]
Podsumowanie
W przedstawionym przykładzie wykonaliśmy kompletne obliczenia charakterystyk geometrycznych złożonego układu składającego się z prostokąta, ćwiartki koła (traktowanej jako figura ujemna) oraz dwuteownika obróconego o kąt . Szczególną uwagę zwrócono na:
- Transformacje geometryczne - zastosowanie transformacji liniowych i kątowych do przeniesienia figur do właściwego układu współrzędnych
- Układ nachylony - obliczenie momentów bezwładności dla dwuteownika z uwzględnieniem jego obrotu
- Figury ujemne - prawidłowe uwzględnienie ćwiartki koła jako figury odejmowanej od układu
- Twierdzenie Steinera - wykorzystanie do obliczenia centralnych momentów bezwładności całego układu
- Weryfikacja - sprawdzenie poprawności obliczeń za pomocą niezmienników i
Poprawność wykonanych obliczeń została potwierdzona przez sprawdzenie niezmienników, co świadczy o prawidłowym wykonaniu wszystkich kroków obliczeniowych dla tego złożonego układu figur.