Momenty dewiacji oraz główne centralne momenty bezwładności

sierpnia 6, 2018

Wprowadzenie

W analizie właściwości geometrycznych przekrojów, oprócz momentów bezwładności, istotną rolę odgrywają momenty dewiacji oraz główne centralne momenty bezwładności. Pojęcia te są niezbędne do prawidłowego projektowania elementów konstrukcyjnych oraz zrozumienia ich zachowania pod obciążeniem.

Moment dewiacji

Moment dewiacji informuje nas o stopniu rozproszenia pola między osiami. Może przyjmować zarówno wartości dodatnie jak i ujemne. Obliczamy go ze wzoru:

D_{xy} = \sum D_{xnyn} + \sum A_n \cdot x \cdot y

Gdzie:

$D_{xy}$ – moment dewiacji układu figur płaskich
$D_{xnyn}$ – moment dewiacji pojedynczej figury
$A_n$ – pole pojedynczej figury
$x$ – różnica odległości pomiędzy osią x środka geometrycznego figury oraz osią, względem której liczymy charakterystyki
$y$ – różnica odległości pomiędzy osią y środka geometrycznego figury oraz osią, względem której liczymy charakterystyki

Znak momentu dewiacji

O tym, czy moment dewiacji będzie dodatni czy ujemny decyduje przewaga pola figury znajdującej się na dodatnich lub ujemnych ćwiartkach układu współrzędnych. Poniższy rysunek ilustruje rozkład pola względem osi układu.

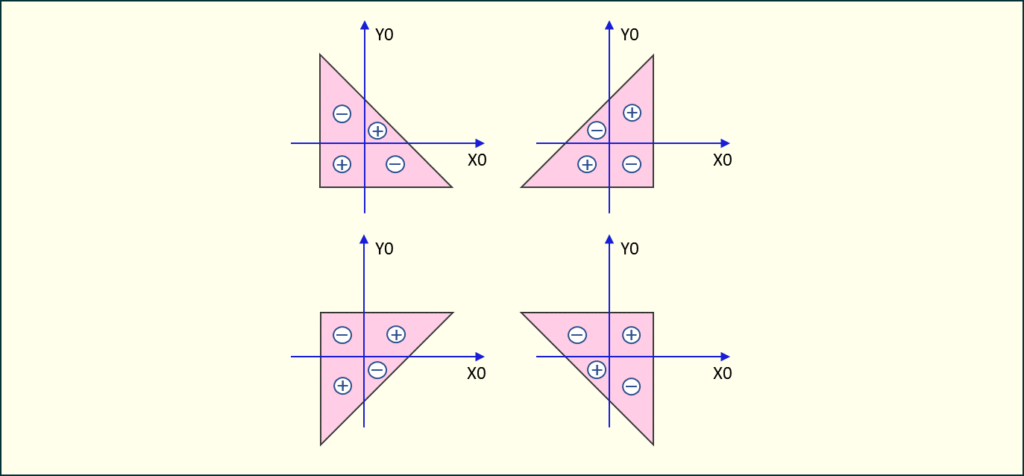
Rys. 1. Rozkład pola figury wwzględem osi układu

Zazwyczaj patrząc na rysunek możemy określić, czy większa część pola znajduje się w ćwiartkach ujemnych lub dodatnich. Jeżeli mamy wątpliwości należy podzielić figurę na mniejsze części i obliczyć różnicę pól dodatnich i ujemnych.

Główne centralne osie bezwładności

Główne centralne osie bezwładności to te, względem których suma momentów dewiacji jest równa zero, a momenty bezwładności osiągają wartości ekstremalne. Są to osie główne obrócone o kąt $\alpha$ .

Kąt obrotu $\alpha$ osi głównych obliczamy ze wzoru:

\operatorname{tg} 2\alpha = \frac{2D_{xy}}{J_y - J_x}

Gdzie:

$D_{xy}$ – moment dewiacji układu figur płaskich
$J_y$ – moment bezwładności względem osi y układu figur płaskich
$J_x$ – moment bezwładności względem osi x układu figur płaskich

Ekstremalne wartości momentów bezwładności

Wartości ekstremalne momentów bezwładności w układzie osi głównych przyjmą wartości:

J_{max} = \frac{J_x + J_y}{2} + \sqrt{\left(\frac{J_x - J_y}{2}\right)^2 + {D_{xy}}^2}

J_{min} = \frac{J_x + J_y}{2} - \sqrt{\left(\frac{J_x - J_y}{2}\right)^2 + {D_{xy}}^2}

Gdzie:

$J_{max}$ – wartość maksymalna momentu bezwładności układu
$J_{min}$ – wartość minimalna momentu bezwładności układu
$D_{xy}$ – moment dewiacji układu figur płaskich
$J_y$ – moment bezwładności względem osi y układu figur płaskich
$J_x$ – moment bezwładności względem osi x układu figur płaskich

Podsumowanie

Moment dewiacji charakteryzuje wzajemne rozmieszczenie pola przekroju względem osi układu współrzędnych i może przyjmować wartości dodatnie lub ujemne w zależności od położenia pola w jego ćwiartkach. Główne centralne osie bezwładności to osie przechodzące przez środek ciężkości przekroju, względem których moment dewiacji jest równy zeru. Względem tych osi momenty bezwładności osiągają wartości ekstremalne: maksymalną i minimalną.

Ostatnia aktualizacja: stycznia 17, 2026

Momenty bezwładności figur płaskich Twierdzenie Steinera