Momenty statyczne figur płaskich
Wprowadzenie
Moment statyczny figury płaskiej to podstawowe pojęcie w mechanice, niezbędne do wyznaczania środka ciężkości figur złożonych oraz obliczania właściwości geometrycznych przekrojów.
Definicja
Momentem statycznym figury płaskiej nazywamy iloczyn pola powierzchni figury oraz odległości jej środka geometrycznego (środka ciężkości) od osi, względem której moment jest liczony.
Gdzie:
- - moment statyczny figury względem osi x
- - moment statyczny figury względem osi y
- - pole powierzchni figury
- , - współrzędne środka ciężkości figury
Moment statyczny może przyjmować wartość dodatnią lub ujemną. Jest wyrażany w jednostkach długości do trzeciej potęgi (m³, cm³, itd.). Jeżeli suma cząstkowych momentów statycznych względem danej osi jest równa zero, to oś ta przechodzi przez środek ciężkości figury.
Wzory na środek ciężkości
Środek ciężkości układu figur możemy obliczyć korzystając z poniższych wzorów:
Przykład obliczeniowy
Załóżmy, że chcemy wyznaczyć środek ciężkości poniższego układu figur.
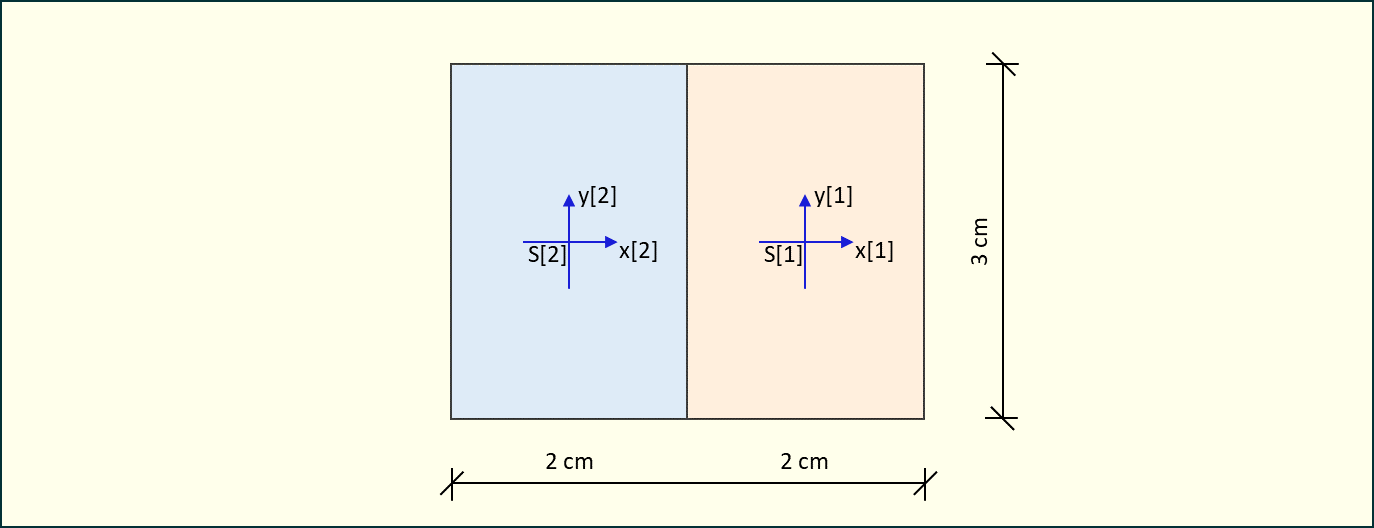
Rys. 1. Układ figur
Najpierw musimy policzyć moment statyczny względem osi, które możemy dobrać wedle uznania, oraz pole całkowite wszystkich figur.
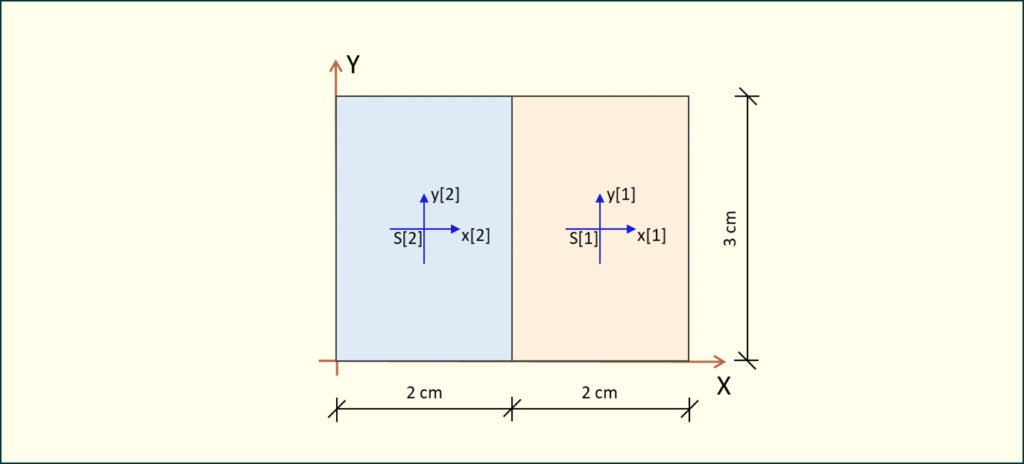
Rys. 2. Układ figur z osią współrzędnych
Figura 1 (prawa)
Zajmijmy się najpierw figurą po prawej.
Figura 2 (lewa)
Teraz obliczmy niezbędne charakterystyki figury po lewej stronie.
Obliczenie środka ciężkości układu
Mając powyższe dane, możemy obliczyć środek ciężkości układu figur płaskich.
Obliczyliśmy współrzędne środka ciężkości układu: oraz .
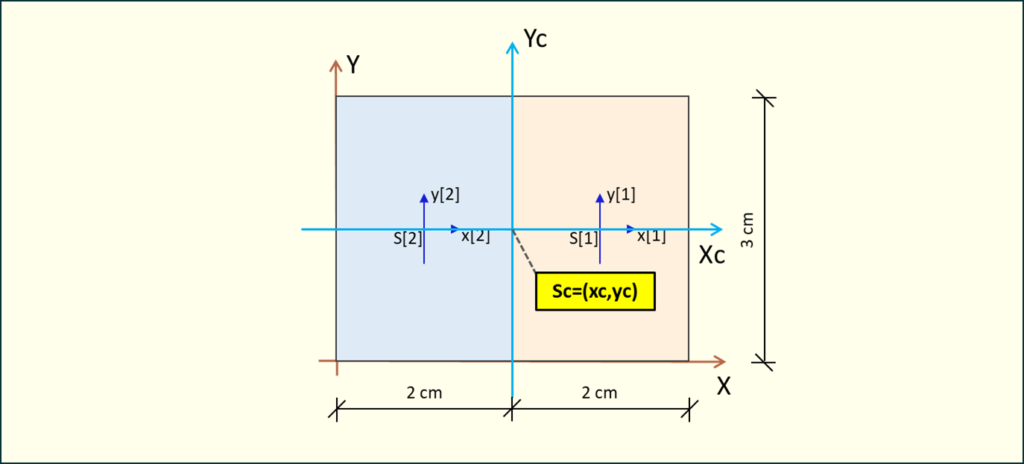
Rys. 3. Położenie środka ciężkości układu figur
Podsumowanie
Momenty statyczne figur płaskich pozwalają na wyznaczenie środka ciężkości układu figur złożonych. Kluczowe kroki to:
- Podział figury złożonej na prostsze elementy
- Wyznaczenie pola powierzchni każdego elementu
- Obliczenie momentów statycznych poszczególnych elementów względem przyjętych osi
- Wyznaczenie współrzędnych środka ciężkości całego układu z odpowiednich wzorów
Metoda ta znajduje szerokie zastosowanie w mechanice konstrukcji, w szczególności przy obliczaniu właściwości geometrycznych przekrojów belek i słupów.