Oś Obojętna i Mimośrodowe Rozciąganie
Obliczenia naprężeń wykonamy na podstawie przykładu nr 2 (cały przykład możesz zobaczyć – tutaj).
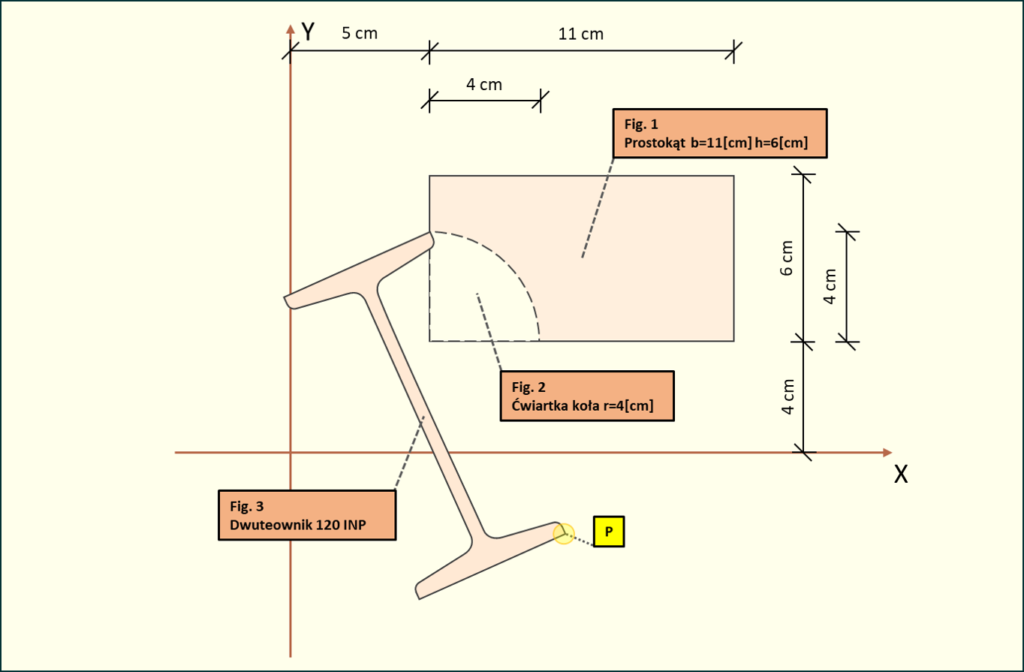
Rys. 1. Układ figur z punktem przyłożenia siły P
1. Relacje wierzchołków Convex
Poszukiwane naprężenia przekroju wyznaczone zostaną we współrzędnych głównych .
Współrzędne wierzchołków Convex przekroju w układzie obliczone będą ze wzorów:
gdzie: to współrzędne w układzie osi centralnych
gdzie: to kąt nachylenia osi głównych
gdzie: ,
Współrzędne wierzchołków Convex w układzie obliczone będą ze wzorów:
gdzie: to współrzędne środka ciężkości w układzie osi
Punkt 1
Punkt 2
Punkt 3
Punkt 4
Punkt 5
Punkt 6
2. Obliczanie naprężeń
3. Wyznaczanie położenia osi obojętnej
Wzór podstawowy równania osi obojętnej we współrzędnych głównych :
Przyjęto parametry i dla ułatwienia obliczeń układu liniowego prostej:
Dzieląc równanie przez otrzymujemy:
Równanie osi obojętnej w układzie osi Głównych :
4. Szkic projektu
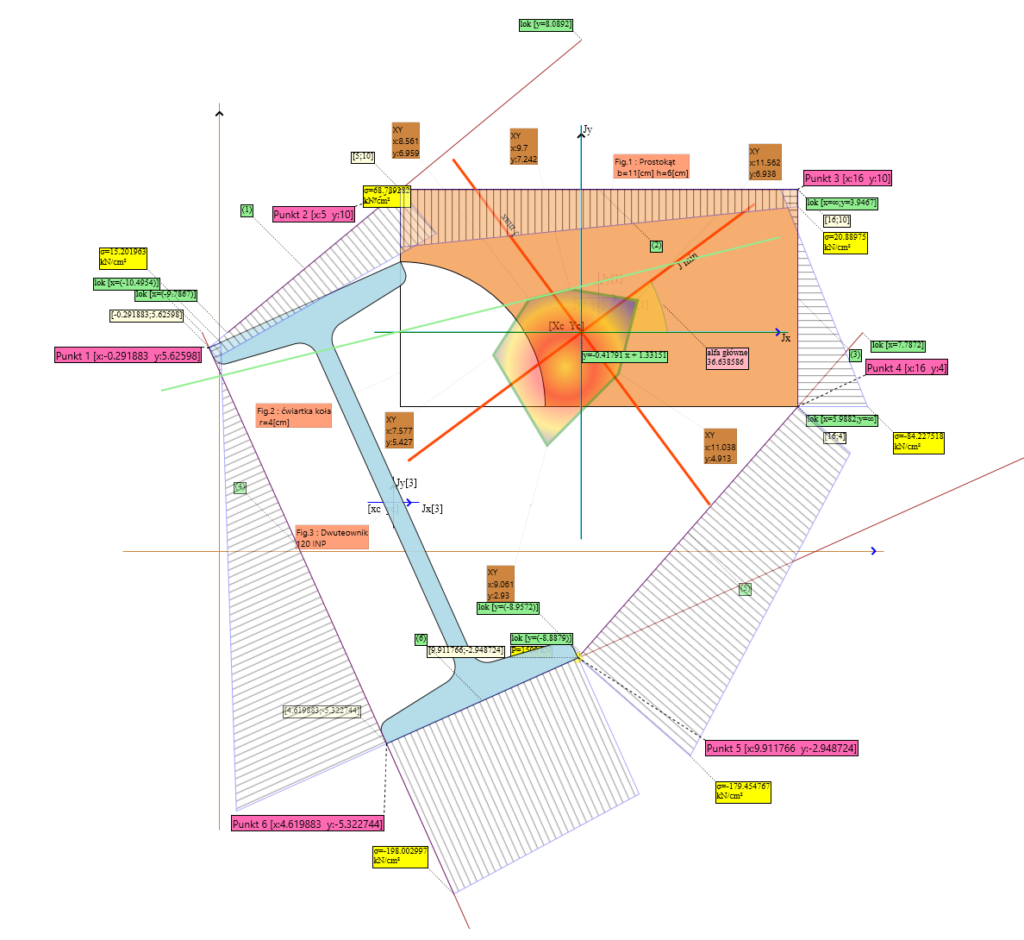
Rys. 2. Szkic projektu z zaznaczoną osią obojętną i rozkładem naprężeń