Kącik Wiedzy
Rdzeń Przekroju

Rdzeń Przekroju

kwietnia 30, 2019

Wprowadzenie

Rdzeń przekroju to obszar wokół środka ciężkości przekroju, w którym może być przyłożona siła normalna bez powodowania naprężeń rozciągających w żadnym punkcie przekroju.

Zadanie: Wyznaczyć rdzeń dla poniższego przekroju.

Obliczenia wykonamy na podstawie przykładu nr 2 (cały przykład możesz zobaczyć w artykule Momenty bezwładności - przykład nr 2).

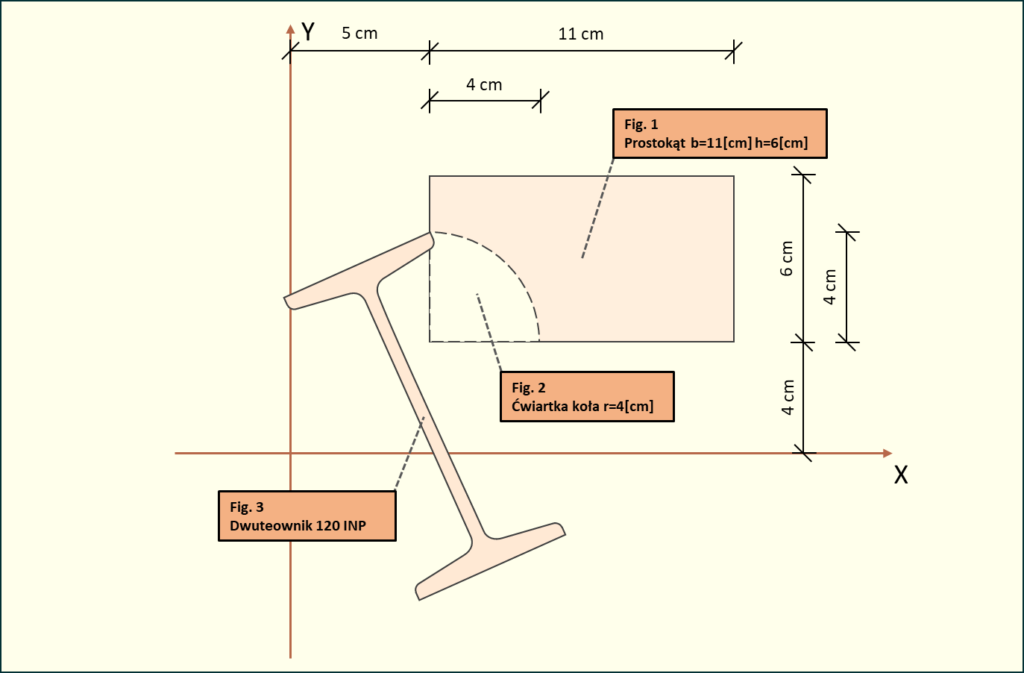
Rys. 1. Układ figur z przykładu nr 2

1. Rdzeń przekroju

1.1. Kwadranty promieni bezwładności

Symbol i2i^2 traktujemy jako całość, nie zaś jako kwadrat liczby:

ix2=JxcA=833,802767,6336=12,3282 [cm2]i_x^2 = \frac{Jx_c}{A} = \frac{833{,}8027}{67{,}6336} = 12{,}3282\ [\mathrm{cm}^2]iy2=JycA=986,250767,6336=14,5823 [cm2]i_y^2 = \frac{Jy_c}{A} = \frac{986{,}2507}{67{,}6336} = 14{,}5823\ [\mathrm{cm}^2]ixy2=DxycA=253,700667,6336=3,7511 [cm2]i_{xy}^2 = \frac{Dxy_c}{A} = \frac{253{,}7006}{67{,}6336} = 3{,}7511\ [\mathrm{cm}^2]
1.2. Relacje wierzchołków rdzenia

Poszukiwany rdzeń przekroju wyznaczony zostanie we współrzędnych centralnych XcX_c, YcY_c.

Współrzędne wierzchołków rdzenia przekroju w układzie XcYcX_cY_c obliczone będą ze wzorów:

xp=−iy2ax−ixy2ayx_p = -\frac{i_y^2}{a_x} - \frac{i_{xy}^2}{a_y}yp=−ix2ay−ixy2axy_p = -\frac{i_x^2}{a_y} - \frac{i_{xy}^2}{a_x}

gdzie axa_x, aya_y oznaczają współrzędne punktów przecięcia przyjętych osi obojętnych z osiami współrzędnych.

Osie współrzędnych przyjęto zgodnie z figurą spełniającą warunek wypukłości (convex).

Punkty przecięcia axa_x, aya_y policzono z warunku funkcji liniowej:

y=a⋅x+by = a \cdot x + bb=y−a⋅xb = y - a \cdot x

gdzie:

  • aa – współczynnik kierunkowy prostej
  • pp – współrzędne początku linii
  • kk – współrzędne końca linii

2. Obliczenia dla poszczególnych osi

2.1. Dla Osi 1 - linia ukośna
p=[5;10]…k=[(−0,2919);5,626]p = [5; 10] \ldots k = [(-0{,}2919); 5{,}626]a=5,626−10(−0,2919)−5=0,8266 cma = \frac{5{,}626 - 10}{(-0{,}2919) - 5} = 0{,}8266\ \mathrm{cm}b=(−10)−0,8266⋅5=5,8672 cmb = (-10) - 0{,}8266 \cdot 5 = 5{,}8672\ \mathrm{cm}ay=5,8672−6,0533+0,8266⋅10,0118=8,0892 cma_y = 5{,}8672 - 6{,}0533 + 0{,}8266 \cdot 10{,}0118 = 8{,}0892\ \mathrm{cm}ax=−8,08920,8266=−9,7867 cma_x = -\frac{8{,}0892}{0{,}8266} = -9{,}7867\ \mathrm{cm}xp=−14,5823(−9,7867)−3,75118,0892=1,0263 cmx_p = -\frac{14{,}5823}{(-9{,}7867)} - \frac{3{,}7511}{8{,}0892} = 1{,}0263\ \mathrm{cm}yp=−12,32828,0892−3,7511(−9,7867)=−1,1407 cmy_p = -\frac{12{,}3282}{8{,}0892} - \frac{3{,}7511}{(-9{,}7867)} = -1{,}1407\ \mathrm{cm}
2.2. Dla Osi 2 - linia pozioma
p=[16;10]…k=[5;10]p = [16; 10] \ldots k = [5; 10]a=∞a = \inftyb=10 cmb = 10\ \mathrm{cm}ay=10−6,0533=3,9467 cma_y = 10 - 6{,}0533 = 3{,}9467\ \mathrm{cm}ax=∞a_x = \inftyxp=−14,5823∞−3,75113,9467=−0,9505 cmx_p = -\frac{14{,}5823}{\infty} - \frac{3{,}7511}{3{,}9467} = -0{,}9505\ \mathrm{cm}yp=−12,32823,9467−3,7511∞=−3,1237 cmy_p = -\frac{12{,}3282}{3{,}9467} - \frac{3{,}7511}{\infty} = -3{,}1237\ \mathrm{cm}
2.3. Dla Osi 3 - linia pionowa
p=[16;4]…k=[16;10]p = [16; 4] \ldots k = [16; 10]a=16 cma = 16\ \mathrm{cm}b=∞b = \inftyay=∞a_y = \inftyax=16−10,0118=5,9882 cma_x = 16 - 10{,}0118 = 5{,}9882\ \mathrm{cm}xp=−14,58235,9882−3,7511∞=−2,4352 cmx_p = -\frac{14{,}5823}{5{,}9882} - \frac{3{,}7511}{\infty} = -2{,}4352\ \mathrm{cm}yp=−12,3282∞−3,75115,9882=−0,6264 cmy_p = -\frac{12{,}3282}{\infty} - \frac{3{,}7511}{5{,}9882} = -0{,}6264\ \mathrm{cm}
2.4. Dla Osi 4 - linia ukośna
p=[(−0,2919);5,626]…k=[4,6199;(−5,3227)]p = [(-0{,}2919); 5{,}626] \ldots k = [4{,}6199; (-5{,}3227)]a=(−5,3227)−5,6264,6199−(−0,2919)=−2,2291 cma = \frac{(-5{,}3227) - 5{,}626}{4{,}6199 - (-0{,}2919)} = -2{,}2291\ \mathrm{cm}b=(−5,626)−(−2,2291)⋅(−0,2919)=4,9753 cmb = (-5{,}626) - (-2{,}2291) \cdot (-0{,}2919) = 4{,}9753\ \mathrm{cm}ay=4,9753−6,0533+(−2,2291)⋅10,0118=−23,3952 cma_y = 4{,}9753 - 6{,}0533 + (-2{,}2291) \cdot 10{,}0118 = -23{,}3952\ \mathrm{cm}ax=−(−23,3952)(−2,2291)=−10,4954 cma_x = -\frac{(-23{,}3952)}{(-2{,}2291)} = -10{,}4954\ \mathrm{cm}xp=−14,5823(−10,4954)−3,7511(−23,3952)=1,5497 cmx_p = -\frac{14{,}5823}{(-10{,}4954)} - \frac{3{,}7511}{(-23{,}3952)} = 1{,}5497\ \mathrm{cm}yp=−12,3282(−23,3952)−3,7511(−10,4954)=0,8844 cmy_p = -\frac{12{,}3282}{(-23{,}3952)} - \frac{3{,}7511}{(-10{,}4954)} = 0{,}8844\ \mathrm{cm}
2.5. Dla Osi 5 - linia ukośna
p=[9,9118;(−2,9487)]…k=[16;4]p = [9{,}9118; (-2{,}9487)] \ldots k = [16; 4]a=4−(−2,9487)16−9,9118=1,1413 cma = \frac{4 - (-2{,}9487)}{16 - 9{,}9118} = 1{,}1413\ \mathrm{cm}b=2,9487−1,1413⋅9,9118=−14,2614 cmb = 2{,}9487 - 1{,}1413 \cdot 9{,}9118 = -14{,}2614\ \mathrm{cm}ay=(−14,2614)−6,0533+1,1413⋅10,0118=−8,8879 cma_y = (-14{,}2614) - 6{,}0533 + 1{,}1413 \cdot 10{,}0118 = -8{,}8879\ \mathrm{cm}ax=−(−8,8879)1,1413=7,7872 cma_x = -\frac{(-8{,}8879)}{1{,}1413} = 7{,}7872\ \mathrm{cm}xp=−14,58237,7872−3,7511(−8,8879)=−1,4505 cmx_p = -\frac{14{,}5823}{7{,}7872} - \frac{3{,}7511}{(-8{,}8879)} = -1{,}4505\ \mathrm{cm}yp=−12,3282(−8,8879)−3,75117,7872=0,9054 cmy_p = -\frac{12{,}3282}{(-8{,}8879)} - \frac{3{,}7511}{7{,}7872} = 0{,}9054\ \mathrm{cm}
2.6. Dla Osi 6 - linia ukośna
p=[4,6199;(−5,3227)]…k=[9,9118;(−2,9487)]p = [4{,}6199; (-5{,}3227)] \ldots k = [9{,}9118; (-2{,}9487)]a=(−2,9487)−(−5,3227)9,9118−4,6199=0,4486 cma = \frac{(-2{,}9487) - (-5{,}3227)}{9{,}9118 - 4{,}6199} = 0{,}4486\ \mathrm{cm}b=5,3227−0,4486⋅4,6199=−7,3953 cmb = 5{,}3227 - 0{,}4486 \cdot 4{,}6199 = -7{,}3953\ \mathrm{cm}ay=(−7,3953)−6,0533+0,4486⋅10,0118=−8,9572 cma_y = (-7{,}3953) - 6{,}0533 + 0{,}4486 \cdot 10{,}0118 = -8{,}9572\ \mathrm{cm}ax=−(−8,9572)0,4486=19,9663 cma_x = -\frac{(-8{,}9572)}{0{,}4486} = 19{,}9663\ \mathrm{cm}xp=−14,582319,9663−3,7511(−8,9572)=−0,3116 cmx_p = -\frac{14{,}5823}{19{,}9663} - \frac{3{,}7511}{(-8{,}9572)} = -0{,}3116\ \mathrm{cm}yp=−12,3282(−8,9572)−3,751119,9663=1,1885 cmy_p = -\frac{12{,}3282}{(-8{,}9572)} - \frac{3{,}7511}{19{,}9663} = 1{,}1885\ \mathrm{cm}

3. Szkic projektu

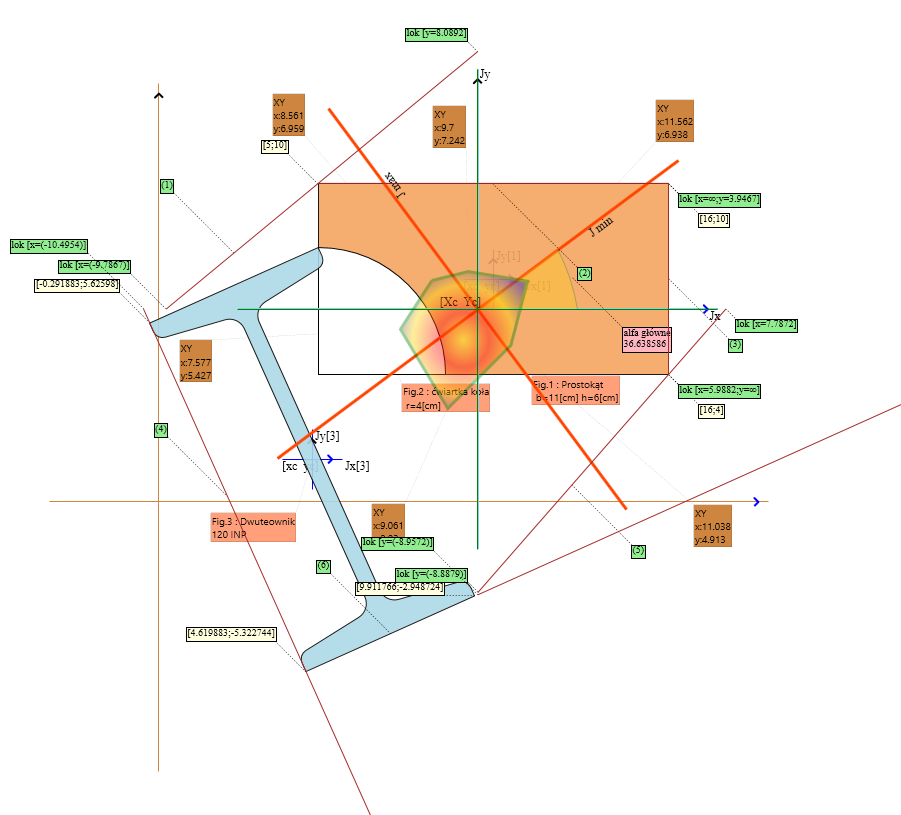
Rys. 2. Rdzeń przekroju - szczegółowy widok z wszystkimi osiami obojętnymi i wierzchołkami rdzenia

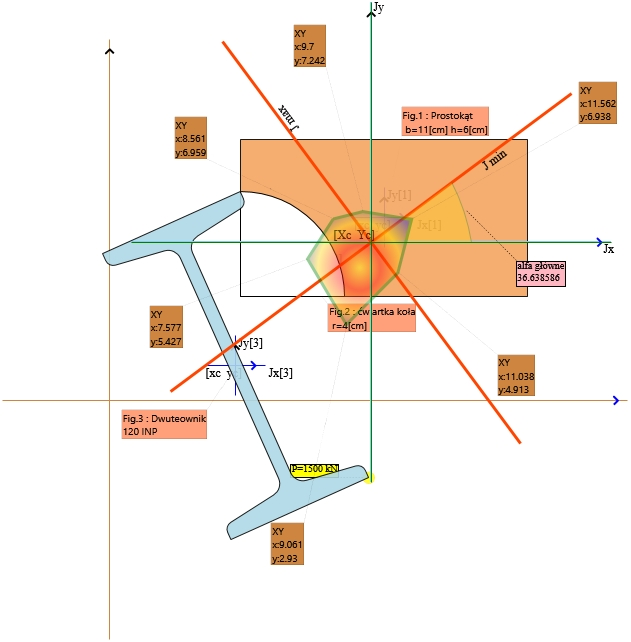
Rys. 3. Rdzeń przekroju - uproszczony widok z zaznaczonym obszarem rdzenia (pomarańczowy)

Ostatnia aktualizacja:
Elipsa BezwładnościOś Obojętna i Mimośrodowe Rozciąganie