Twierdzenie Steinera
Wprowadzenie
Twierdzenie Steinera (zwane również twierdzeniem o osi równoległych lub twierdzeniem Huygensa–Steinera) jest fundamentalnym narzędziem w mechanice konstrukcji. Umożliwia ono obliczanie geometrycznych momentów bezwładności figur płaskich, a także układów figur, względem osi równoległych do osi przechodzących przez środek ciężkości przekroju.
Wzory twierdzenia Steinera
Aby obliczyć momenty bezwładności względem takiej osi, można skorzystać z następujących zależności:
Gdzie:
- , – całkowity moment bezwładności względem osi x oraz y
- , – moment bezwładności pojedynczej figury względem osi przechodzącej przez jej geometryczny środek
- – pole figury płaskiej
- , – odległości pomiędzy osiami znajdującymi się w geometrycznym środku figury oraz osiami, względem których obliczamy moment bezwładności
Przykład obliczeniowy
Postarajmy się obliczyć moment bezwładności kwadratu względem dowolnej osi.
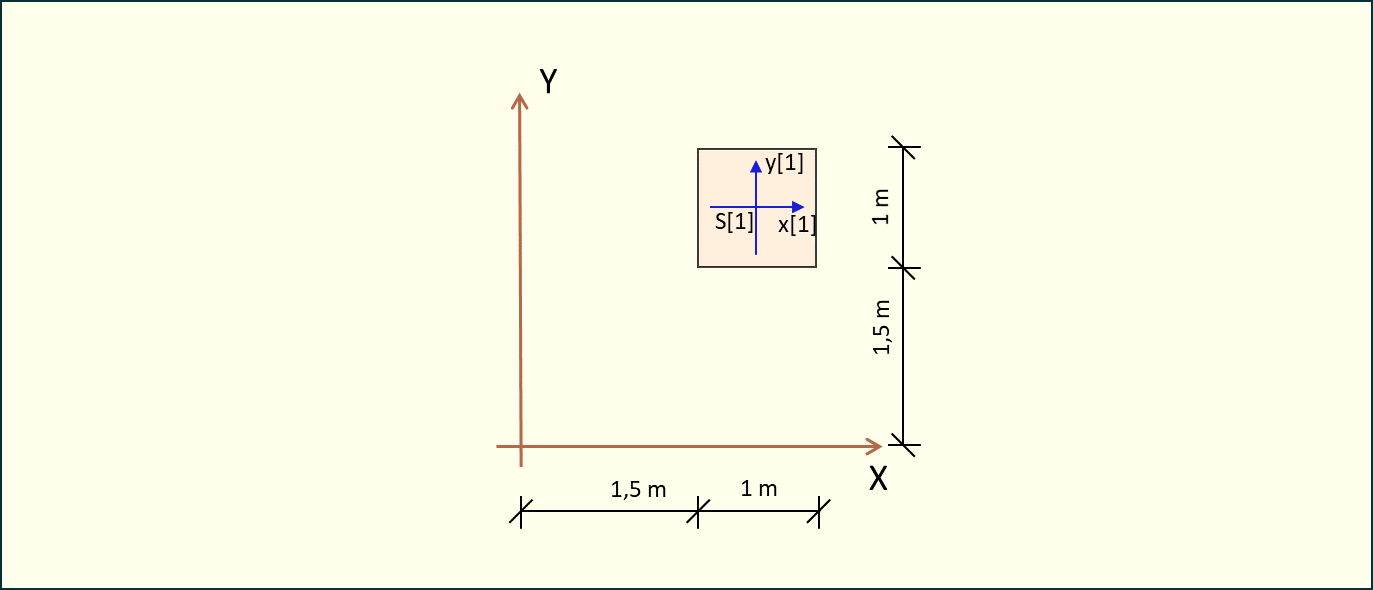
Rys. 1. Przykład obliczeniowy
Krok 1: Moment bezwładności względem osi centralnych
Najpierw policzmy moment bezwładności kwadratu względem jego geometrycznego środka. Dla większości figur płaskich wzory można znaleźć w tablicach inżynierskich.
Gdzie:
- – długość boku kwadratu (1 m)
Krok 2: Pole kwadratu
Teraz musimy policzyć pole kwadratu:
Krok 3: Odległości między osiami
Następnie obliczamy odległości i będące odległością między środkiem kwadratu a początkiem układu współrzędnych.
Z rysunku odczytujemy, że środek kwadratu znajduje się w odległości:
Krok 4: Obliczenie momentów bezwładności
Mając wszystkie potrzebne dane możemy zatem obliczyć potrzebne nam momenty bezwładności względem osi X i Y korzystając z twierdzenia Steinera:
Podsumowanie
Twierdzenie Steinera umożliwia efektywne obliczanie momentów bezwładności figur płaskich względem osi równoległych do osi centralnych przechodzących przez środek ciężkości przekroju. Kluczowe znaczenie ma poprawne wyznaczenie odległości między osiami oraz znajomość momentów bezwładności względem osi centralnych. Twierdzenie to znajduje szerokie zastosowanie przy wyznaczaniu charakterystyk geometrycznych złożonych przekrojów, w których momenty bezwładności poszczególnych elementów przenoszone są do wspólnego układu współrzędnych.